题目内容
设数列{an}满足a1=1,a2=2,an=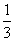 (an-1+2an-2)(n=3,4,…)。数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1≤bm+bm+1+…+bm+k≤1,
(an-1+2an-2)(n=3,4,…)。数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1≤bm+bm+1+…+bm+k≤1,
(1)求数列{an}和{bn}的通项公式;
(2)记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn.
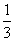 (an-1+2an-2)(n=3,4,…)。数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1≤bm+bm+1+…+bm+k≤1,
(an-1+2an-2)(n=3,4,…)。数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1≤bm+bm+1+…+bm+k≤1,(1)求数列{an}和{bn}的通项公式;
(2)记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn.
解:(1)由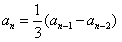 得
得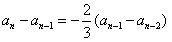 (n≥3),
(n≥3),
又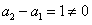 ,
,
∴数列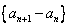 是首项为1公比为
是首项为1公比为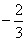 的等比数列,
的等比数列,
∴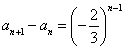 ,
,
∴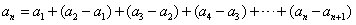
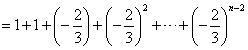
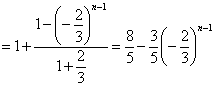 ,
,
由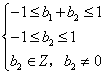 得b2=-1,
得b2=-1,
由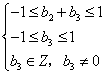 得b3=1,
得b3=1,
同理可得当n为偶数时,bn=-1;当n为奇数时,bn=1;
因此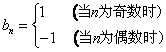 。
。
(2) ,
,
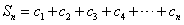 ,
,
当n为奇数时,
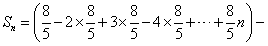
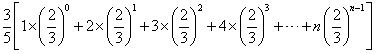
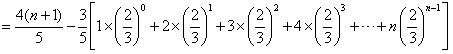 ;
;
当n为偶数时,
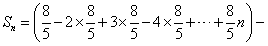
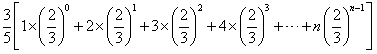
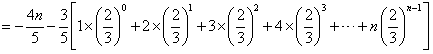 ,
,
令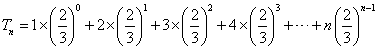 , ①
, ①
①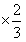 得:
得: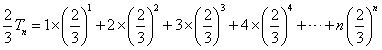 ,②
,②
①-②得:
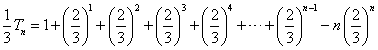
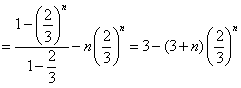 ,
,
∴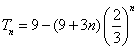 ;
;
因此,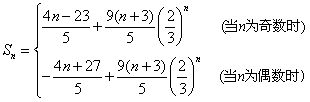 。
。
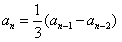 得
得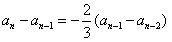 (n≥3),
(n≥3),又
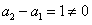 ,
,∴数列
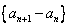 是首项为1公比为
是首项为1公比为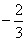 的等比数列,
的等比数列,∴
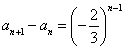 ,
,∴
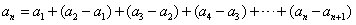
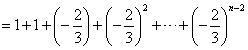
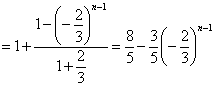 ,
,由
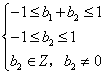 得b2=-1,
得b2=-1,由
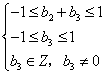 得b3=1,
得b3=1,同理可得当n为偶数时,bn=-1;当n为奇数时,bn=1;
因此
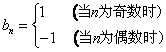 。
。(2)
 ,
,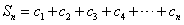 ,
,当n为奇数时,
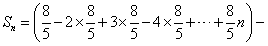
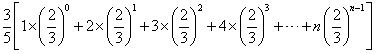
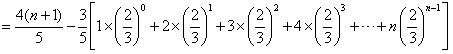 ;
;当n为偶数时,
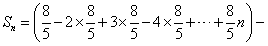
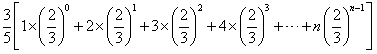
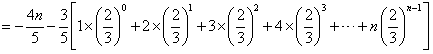 ,
,令
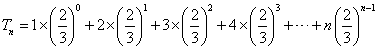 , ①
, ① ①
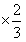 得:
得: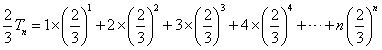 ,②
,②①-②得:
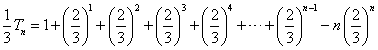
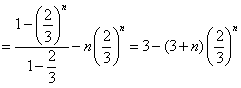 ,
,∴
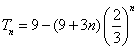 ;
;因此,
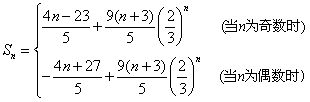 。
。 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|