题目内容
已知函数f(x)=2x,g(x)= +2.
+2.
(1)求函数g(x)的值域;
(2)求满足方程f(x)-g(x)=0的x的值.
解:(1)g(x)= +2=(
+2=( )|x|+2,
)|x|+2,
因为|x|≥0,所以0<( )|x|≤1,即2<g(x)≤3,
)|x|≤1,即2<g(x)≤3,
故g(x)的值域是(2,3].
(2)由f(x)-g(x)=0得2x- -2=0,
-2=0,
当x≤0时,显然不满足方程,即只有x>0满足2x-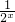 -2=0,
-2=0,
整理得(2x)2-2•2x-1=0,(2x-1)2=2,
故2x=1± ,
,
因为2x>0,所以2x=1+ ,即x=log2(1+
,即x=log2(1+ ).
).
分析:(1)求函数g(x)的值域先研究其性质,由于|x|≥0,故得0<( )|x|≤1,代入g(x)=
)|x|≤1,代入g(x)= +2求值域,此方法先求局部取值范围再研究整体的值域.
+2求值域,此方法先求局部取值范围再研究整体的值域.
(2)将f(x)=2x,g(x)= +2代入方程f(x)-g(x)=0得2x-
+2代入方程f(x)-g(x)=0得2x- -2=0,解此指数型方程求x的值
-2=0,解此指数型方程求x的值
点评:本题考点是指数函数综合题,考查求函数的值域与解指数型方程,解题过程中要注意指数函数的值域是(0,+∞)这一隐含条件.
 +2=(
+2=( )|x|+2,
)|x|+2,因为|x|≥0,所以0<(
 )|x|≤1,即2<g(x)≤3,
)|x|≤1,即2<g(x)≤3,故g(x)的值域是(2,3].
(2)由f(x)-g(x)=0得2x-
 -2=0,
-2=0,当x≤0时,显然不满足方程,即只有x>0满足2x-
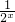 -2=0,
-2=0,整理得(2x)2-2•2x-1=0,(2x-1)2=2,
故2x=1±
 ,
,因为2x>0,所以2x=1+
 ,即x=log2(1+
,即x=log2(1+ ).
).分析:(1)求函数g(x)的值域先研究其性质,由于|x|≥0,故得0<(
 )|x|≤1,代入g(x)=
)|x|≤1,代入g(x)= +2求值域,此方法先求局部取值范围再研究整体的值域.
+2求值域,此方法先求局部取值范围再研究整体的值域.(2)将f(x)=2x,g(x)=
 +2代入方程f(x)-g(x)=0得2x-
+2代入方程f(x)-g(x)=0得2x- -2=0,解此指数型方程求x的值
-2=0,解此指数型方程求x的值点评:本题考点是指数函数综合题,考查求函数的值域与解指数型方程,解题过程中要注意指数函数的值域是(0,+∞)这一隐含条件.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目