题目内容
已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=1，P为腰DC上的动点，则|2
+3
|的最小值为________．
7
分析：根据题意，设CD=a，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（2，0），B（1，a），C（0，a），D（0，0），设P（0，b）（0≤b≤a），求出2+3，根据向量模的计算公式，即可求得|2+3|，利用完全平方式非负，即可求得其最小值．
解答：
解：如图，以直线DA，DC分别为x，y轴建立平面直角坐标系，设CD=a，
则A（2，0），B（1，a），C（0，a），D（0，0）
设P（0，b）（0≤b≤a）
则=（2，-b），=（1，a-b），
∴2+3=（7，3a-5b）
∴|2+3|=|（7，3a-5b）|=
≥7．
故答案为：7．
点评：此题是个基础题．考查向量在几何中的应用，以及向量模的求法，同时考查学生灵活应用知识分析解决问题的能力．
分析：根据题意，设CD=a，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（2，0），B（1，a），C（0，a），D（0，0），设P（0，b）（0≤b≤a），求出2
+3，根据向量模的计算公式，即可求得|2+3|，利用完全平方式非负，即可求得其最小值．解答：
解：如图，以直线DA，DC分别为x，y轴建立平面直角坐标系，设CD=a，则A（2，0），B（1，a），C（0，a），D（0，0）
设P（0，b）（0≤b≤a）
则
=（2，-b），=（1，a-b），∴2
+3=（7，3a-5b）∴|2
+3|=|（7，3a-5b）|=≥7．故答案为：7．
点评：此题是个基础题．考查向量在几何中的应用，以及向量模的求法，同时考查学生灵活应用知识分析解决问题的能力．
练习册系列答案
相关题目
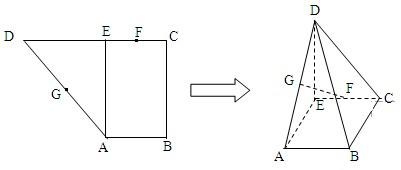
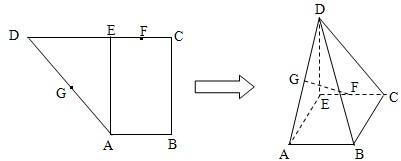
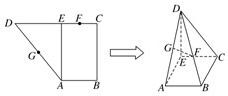已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=1，BC=2，CD=1+
已知直角梯形ABCD中，AB∥CD，∠BAD=90°，且AB=2，AD=3，CD=1，点E、F分别在AD、BC上，满足
如图，已知直角梯形ABCD的上底BC=