题目内容
.(本小题满分16分)
平面直角坐标系xOy中,已知圆M经过F1(0,-c),F2(0,c),A(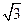 c,0)三点,其中c>0
c,0)三点,其中c>0
(1)求圆M的标准方程(用含c的式子表示);
(2)已知椭圆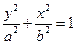
 (其中
(其中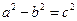 )的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
)的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
求椭圆离心率的取值范围;
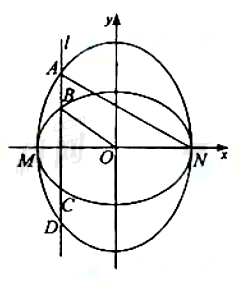
若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由。
平面直角坐标系xOy中,已知圆M经过F1(0,-c),F2(0,c),A(
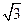 c,0)三点,其中c>0
c,0)三点,其中c>0(1)求圆M的标准方程(用含c的式子表示);
(2)已知椭圆
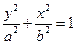
 (其中
(其中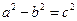 )的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
)的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。求椭圆离心率的取值范围;
若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由。
.设圆M: 
 3分
3分
圆M: 5分
5分
(2)① ,又
,又 ,由题意
,由题意
7分
 即
即 10分
10分
②由① 则
则

 ①,
①, ②, 13分
②, 13分
由①②的两直线的交点 易知
易知 为定值,
为定值,
 点
点 在定直线
在定直线 上 16分
上 16分

 3分
3分 圆M:
 5分
5分(2)①
 ,又
,又 ,由题意
,由题意
7分
 即
即 10分
10分②由①
 则
则

 ①,
①, ②, 13分
②, 13分由①②的两直线的交点
 易知
易知 为定值,
为定值, 点
点 在定直线
在定直线 上 16分
上 16分略

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
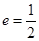 ,求
,求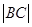 与
与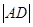 的比值;
的比值;





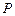 是椭圆
是椭圆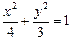 上一动点,点
上一动点,点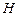 是点
是点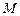 在
在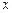 轴上的射影,坐标平面
轴上的射影,坐标平面 内动点
内动点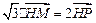 (
( 为坐标原点),设动点
为坐标原点),设动点 .
.
 的直线
的直线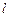 交曲线
交曲线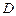 ,
,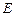 两点,且
两点,且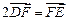 ,点
,点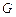 ,求直线
,求直线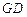 的方程.
的方程.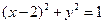 都相切,则双曲线C的离心率是____;
都相切,则双曲线C的离心率是____;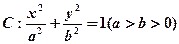 的焦距为2,点
的焦距为2,点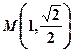 在椭圆
在椭圆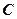 上,
上,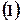 求椭圆
求椭圆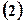 若过点
若过点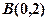 的直线与
的直线与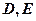 (
(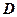 在
在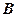 、
、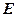 之间);
之间);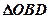 与
与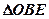 面积之比的取值范围.
面积之比的取值范围.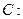
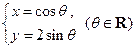 经过点
经过点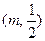 ,则
,则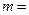 ______,离心率
______,离心率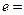 ______.
______.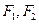 ,离心率为
,离心率为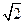 ,且过点
,且过点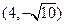 ,
,
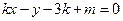 (其中
(其中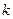 为参数)所过的定点
为参数)所过的定点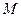 恰在双曲线上,求证:
恰在双曲线上,求证: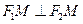 。
。