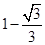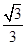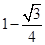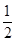题目内容
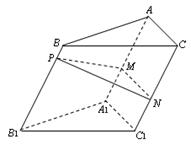
(本小题满分13分)如图,正方形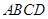 所在平面与三角形
所在平面与三角形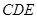 所在平面相交于
所在平面相交于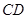 ,
,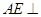 平面
平面 ,且
,且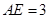 ,
,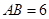
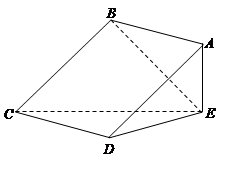
(1)求证: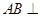 平面
平面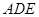 ;
;
(2)求凸多面体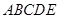 的体积.
的体积.
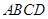 所在平面与三角形
所在平面与三角形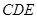 所在平面相交于
所在平面相交于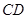 ,
,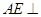 平面
平面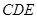 ,且
,且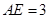 ,
,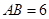
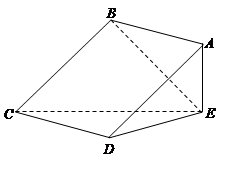
(1)求证:
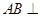 平面
平面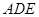 ;
;(2)求凸多面体
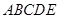 的体积.
的体积.(1)见解析;(2)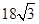
本试题主要考查了多面体的体积的求解以及线面垂直的判定定理的运用。
(1)要证明AB垂直于平面,则利用AB//CD,通过证明CD垂直于平面得到证明。
(2)对多面体的体积可知看作是四棱锥的体积,结合分割的思想转化为两个三棱锥的体积和,得到结论。
(1)证明:∵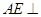 平面
平面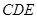 ,
,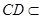 平面
平面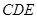 ,
,
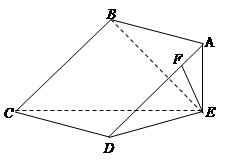
∴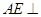
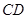 .
.
在正方形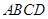 中,
中,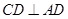 ,
,
∵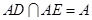 ,∴
,∴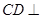 平面
平面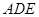 .
.
∵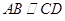 ,
,
∴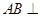 平面
平面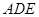 .………………7分
.………………7分
(2)解法1:在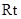 △
△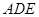 中,
中,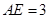 ,
,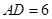 ,
,
∴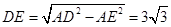 .
.
过点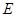 作
作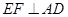 于点
于点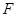 ,
,
∵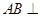 平面
平面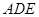 ,
,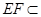 平面
平面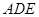 ,
,
∴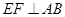 .
.
∵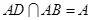 ,
,
∴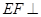 平面
平面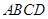 .
.
∵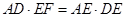 ,
,
∴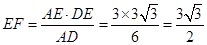 .
.
又正方形 的面积
的面积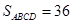 ,
,
∴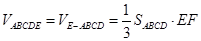
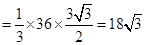 .
.
故所求凸多面体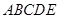 的体积为
的体积为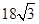 .………………14分
.………………14分
解法2:在 △
△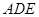 中,
中,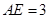 ,
,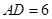 ,
,
∴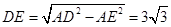 .
.
连接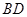 ,则凸多面体
,则凸多面体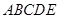 分割为三棱锥
分割为三棱锥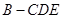
和三棱锥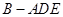 .
.
由(1)知,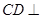
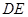 .
.
∴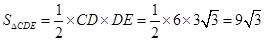 .
.
又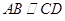 ,
,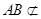 平面
平面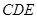 ,
,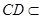 平面
平面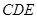 ,
,
∴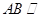 平面
平面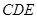 .
.
∴点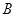 到平面
到平面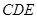 的距离为
的距离为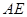 的长度.
的长度.
∴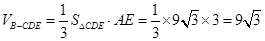 .
.
∵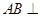 平面
平面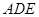 ,
,
∴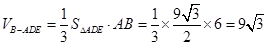 .
.
∴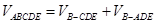
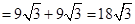 .
.
故所求凸多面体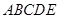 的体积为
的体积为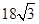 .………………14分
.………………14分
(1)要证明AB垂直于平面,则利用AB//CD,通过证明CD垂直于平面得到证明。
(2)对多面体的体积可知看作是四棱锥的体积,结合分割的思想转化为两个三棱锥的体积和,得到结论。
(1)证明:∵
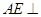 平面
平面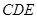 ,
,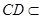 平面
平面 ,
,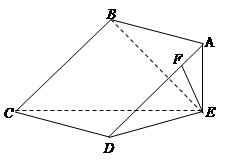
∴
 .
. 在正方形
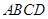 中,
中,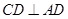 ,
,∵
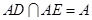 ,∴
,∴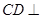 平面
平面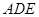 .
.∵
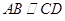 ,
,∴
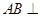 平面
平面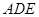 .………………7分
.………………7分(2)解法1:在
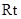 △
△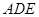 中,
中,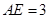 ,
,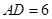 ,
,∴
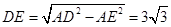 .
.过点
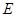 作
作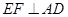 于点
于点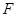 ,
,∵
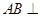 平面
平面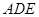 ,
,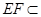 平面
平面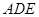 ,
,∴
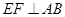 .
. ∵
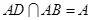 ,
,∴
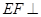 平面
平面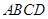 .
.∵
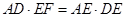 ,
,∴
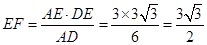 .
.又正方形
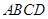 的面积
的面积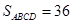 ,
, ∴
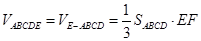
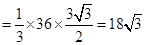 .
.故所求凸多面体
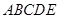 的体积为
的体积为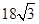 .………………14分
.………………14分解法2:在
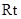 △
△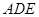 中,
中,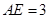 ,
,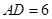 ,
,∴
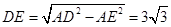 .
. 连接
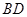 ,则凸多面体
,则凸多面体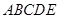 分割为三棱锥
分割为三棱锥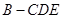
和三棱锥
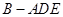 .
. 由(1)知,
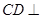
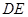 .
.∴
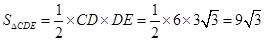 .
.又
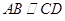 ,
,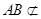 平面
平面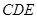 ,
,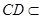 平面
平面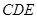 ,
,∴
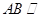 平面
平面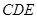 .
.∴点
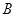 到平面
到平面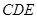 的距离为
的距离为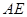 的长度.
的长度.∴
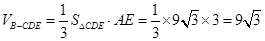 .
. ∵
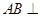 平面
平面 ,
,∴
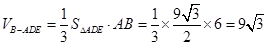 .
.∴
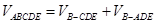
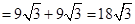 .
.故所求凸多面体
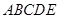 的体积为
的体积为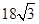 .………………14分
.………………14分
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
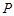 为斜三棱柱
为斜三棱柱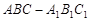 的侧棱
的侧棱 上一点,
上一点,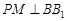 交
交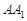 于点
于点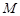 ,
,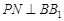 交
交 于点
于点 .
.
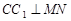 ;
;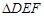 中有余弦定理:
中有余弦定理: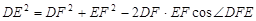 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)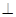 AD且AB=AD=
AD且AB=AD=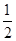 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
 中
中 且
且 .
.
 .
. 与平面
与平面 所成的角.
所成的角. 的平面角.
的平面角.
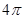 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积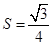 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为 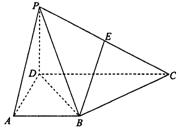
 绕点
绕点 逆时针旋转
逆时针旋转 到正方形
到正方形 ,图中阴影部分的面积为( )
,图中阴影部分的面积为( )