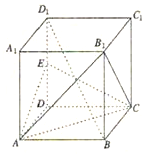
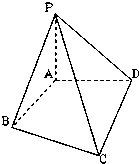
题目内容
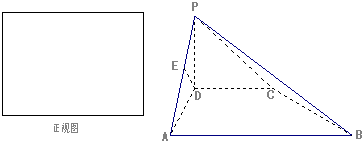
如图,已知PA⊥面ABCD,PA=AB=AD=
CD,∠BAD=∠ADC=90°
(1)在面PCD上找一点M,使BM⊥面PCD;
(2)求由面PBC与面PAD所成角的二面角的余弦值.
| 1 |
| 2 |
(1)在面PCD上找一点M,使BM⊥面PCD;
(2)求由面PBC与面PAD所成角的二面角的余弦值.

(1)M为PC的中点,设PD中点为N,则MN=
CD,且MN∥
CD,∴MN=AB,MN∥AB.
再由 PA=AB=AD=
CD,可得ABMN为平行四边形,∴BM∥AN.
可得∠PAD=90°,∴AN⊥PD,又CD⊥AN,∴AN⊥面PCD,∴BM⊥面PCD.…(6分)
(2)延长CB交DA于E,∵AB=
CD,且AB∥
CD,∴AE=AD=PA,∴PD⊥PE.
又∴PE⊥CD,∴PE⊥面PCD,∴∠CPD为二面角C-PE-D的平面角.
再由PD=
AD,CD=2AD,可得tan∠CPD=
,
∴cos∠CPD=
.…(12分)

| 1 |
| 2 |
| 1 |
| 2 |
再由 PA=AB=AD=
| 1 |
| 2 |
可得∠PAD=90°,∴AN⊥PD,又CD⊥AN,∴AN⊥面PCD,∴BM⊥面PCD.…(6分)
(2)延长CB交DA于E,∵AB=
| 1 |
| 2 |
| 1 |
| 2 |
又∴PE⊥CD,∴PE⊥面PCD,∴∠CPD为二面角C-PE-D的平面角.
再由PD=
| 2 |
| 2 |
∴cos∠CPD=
| ||
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目