题目内容
已知函数![]() (
(![]() 且
且![]() ).
).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)记函数![]() 的图象为曲线
的图象为曲线![]() .设点
.设点![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点.如果在曲线
上的不同两点.如果在曲线![]() 上存在点
上存在点![]() ,使得:①
,使得:①![]() ;②曲线
;②曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,则称函数
,则称函数![]() 存在“中值相依切线”.
存在“中值相依切线”.
试问:函数![]() 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
解:(Ⅰ)显然函数![]() 的定义域是
的定义域是![]() . …………1分
. …………1分
由已知得,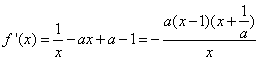 . …………2分
. …………2分
⑴当![]() 时, 令
时, 令![]() ,解得
,解得![]() ; 令
; 令![]() ,解得
,解得![]() .
.
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减. …………3分
上单调递减. …………3分
⑵当![]() 时,
时,
①当![]() 时,即
时,即![]() 时, 令
时, 令![]() ,解得
,解得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]() .
.
所以,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;…………4分
上单调递减;…………4分
②当![]() 时,即
时,即![]() 时, 显然,函数
时, 显然,函数![]() 在
在![]() 上单调递增; ………5分
上单调递增; ………5分
③当![]() 时,即
时,即![]() 时, 令
时, 令![]() ,解得
,解得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]() .
.
所以,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.…………6分
上单调递减.…………6分
综上所述,⑴当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
⑵当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
⑶当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
⑷当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
……………7分
(Ⅱ)假设函数![]() 存在“中值相依切线”.
存在“中值相依切线”.
设![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点,且
上的不同两点,且![]() ,
,
则![]() ,
,![]() .
.
![]()
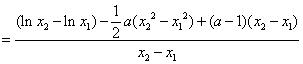
![]() …………8分
…………8分
曲线在点![]() 处的切线斜率
处的切线斜率
![]()
![]()
![]() , …………9分
, …………9分
依题意得:![]()
![]() .
.
化简可得: ![]()
![]() ,
,
即![]() =
=![]()
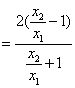 . …………11分
. …………11分
设![]() (
(![]() ),上式化为:
),上式化为:![]() ,
,
即![]() . …………12分
. …………12分
令![]() ,
,![]()
![]()
![]() .
.
因为![]() ,显然
,显然![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
显然有![]() 恒成立.
恒成立.
所以在![]() 内不存在
内不存在![]() ,使得
,使得![]() 成立.
成立.
综上所述,假设不成立.所以,函数![]() 不存在“中值相依切线”.……………14分
不存在“中值相依切线”.……………14分

 ,且
,且 在
在 和
和 处取得极值.
处取得极值. ,是否存在实数
,是否存在实数 ,使得曲线
,使得曲线 与
与 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出
 ,且
,且
 的值
的值 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明 ,若
,若 且
且 ,则下列不等式中正确的是( )
,则下列不等式中正确的是( ) B.
B.
 C.
C.
 D.
D.
 ,且
,且 ,
, .那么下列命题中真命题的序号是
.那么下列命题中真命题的序号是 的最大值为
的最大值为 ②
②  在
在 上是减函数
④
上是减函数
④ 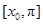 上是减函数
上是减函数 ,且
,且 是奇函数。
是奇函数。 ,
, 的值;
的值; 的单调区间。
的单调区间。