题目内容
已知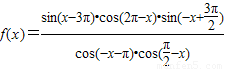
(1)若x是第三象限的角,且sin(-x-π)=
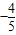 ,求f(x)的值.
,求f(x)的值.(2)求函数
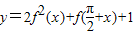 的值域.
的值域.
【答案】分析:(1)根据诱导公式化简,得f(x)=-cosx.再由sin(-x-π)=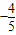 得sinx=
得sinx=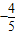 ,利用同角三角函数的关系结合x是第三象限的角,算出f(x)=-cosx=
,利用同角三角函数的关系结合x是第三象限的角,算出f(x)=-cosx= ;
;
(1)由f(x)表达式,结合诱导公式与同角三角函数的平方关系化简,得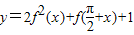 ═-2(sinx-
═-2(sinx- )2+
)2+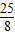 ,再由二次函数的单调性结合sinx∈[-1,1],即可算出所求函数的值域.
,再由二次函数的单调性结合sinx∈[-1,1],即可算出所求函数的值域.
解答:解:根据题意,得
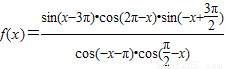
=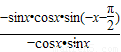 =sin(-x-
=sin(-x-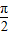 )=-sin(
)=-sin(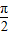 -x)=-cosx
-x)=-cosx
(1)∵x是第三象限的角,且sin(-x-π)=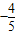 ,
,
∴sinx=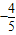 ,可得cosx=-
,可得cosx=-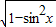 =-
=- ,
,
由此可得f(x)=-cosx= ;
;
(2)函数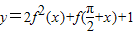 =2cos2x-cos(
=2cos2x-cos(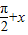 )+1
)+1
即y=2cos2x+sinx+1=-2(sinx- )2+
)2+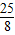
∵sinx∈[-1,1],
∴当sinx= 时,函数的最大值为
时,函数的最大值为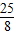 ;当sinx=-1时,函数的最小值为0
;当sinx=-1时,函数的最小值为0
因此,函数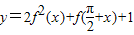 的值域为[0,
的值域为[0,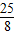 ]
]
点评:本题题将一个三角函数式化简,求特殊函数值并求另一函数的值域.着重考查了诱导公式、同角三角函数的基本关系与二次函数的图象与性质等知识,属于中档题.
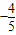 得sinx=
得sinx=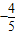 ,利用同角三角函数的关系结合x是第三象限的角,算出f(x)=-cosx=
,利用同角三角函数的关系结合x是第三象限的角,算出f(x)=-cosx= ;
;(1)由f(x)表达式,结合诱导公式与同角三角函数的平方关系化简,得
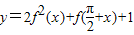 ═-2(sinx-
═-2(sinx- )2+
)2+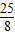 ,再由二次函数的单调性结合sinx∈[-1,1],即可算出所求函数的值域.
,再由二次函数的单调性结合sinx∈[-1,1],即可算出所求函数的值域.解答:解:根据题意,得
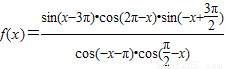
=
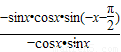 =sin(-x-
=sin(-x-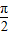 )=-sin(
)=-sin(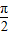 -x)=-cosx
-x)=-cosx(1)∵x是第三象限的角,且sin(-x-π)=
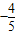 ,
,∴sinx=
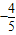 ,可得cosx=-
,可得cosx=-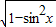 =-
=- ,
,由此可得f(x)=-cosx=
 ;
;(2)函数
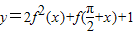 =2cos2x-cos(
=2cos2x-cos(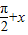 )+1
)+1即y=2cos2x+sinx+1=-2(sinx-
 )2+
)2+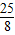
∵sinx∈[-1,1],
∴当sinx=
 时,函数的最大值为
时,函数的最大值为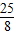 ;当sinx=-1时,函数的最小值为0
;当sinx=-1时,函数的最小值为0因此,函数
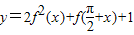 的值域为[0,
的值域为[0,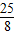 ]
]点评:本题题将一个三角函数式化简,求特殊函数值并求另一函数的值域.着重考查了诱导公式、同角三角函数的基本关系与二次函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目