题目内容
已知定义在![]() 上的函数
上的函数![]() ,满足条件:①
,满足条件:①![]() ,②对非零实数
,②对非零实数![]() ,都有
,都有![]() .
.
(1)求函数 的解析式;
的解析式;
(2)设函数![]() ,直线
,直线![]() 分别与函数
分别与函数![]() ,
,![]() 交于
交于![]() 、
、![]() 两点,(其中
两点,(其中![]() ),求
),求![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:当
项和,求证:当![]() 时,
时,![]() .
.
解:(1)当![]() 时,
时,![]()
故 ![]() 两式联立可得,
两式联立可得,![]()
又当![]() 时,有
时,有![]() ;∴
;∴![]() 。…………………4分
。…………………4分

所以, 。……………8分
。……………8分
(3)由(2)知![]() ,
, ![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]()
……,![]()
累加得: ![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]() 。…………………12分
。…………………12分

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数 的一个极值点,求
的一个极值点,求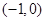 上是增函数,求实数
上是增函数,求实数 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数 上的函数
上的函数 ,则曲线
,则曲线 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B.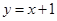 C.
C. D.
D.
 上的函数
上的函数 ,其中
,其中 为常数.
为常数. 是函数
是函数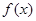 的一个极值点,求
的一个极值点,求 上是增函数,求
上是增函数,求 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 满足
满足 ,
, ,则不等式
,则不等式 的解集为
.
的解集为
.