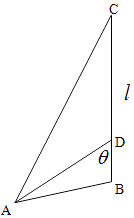Question

【题目】如图，在四边形ABCD中，∠ABC= ，AB：BC=2：3， ．

（1）求sin∠ACB的值；
（2）若 ，CD=1，求△ACD的面积．

Answer 1

【答案】
（1）解：∵∠ABC= ，AB：BC=2：3， ，可得：AB= ，

∴在△ABC中，由余弦定理AC2=AB2+BC2﹣2ABBCcos∠ABC，可得：7= +BC2﹣ ，

∴解得：BC=3，AB=2，

∴由正弦定理可得：sin∠ACB= = =

（2）解：∵由（1）及余弦定理可得：

cos∠ACB= = = ，

∴sin = （cos∠ACB+sin∠ACB）

= （ + ），

∴S△ACD= ACCDsin∠ACD= 1× ×（ + ）= ．

【解析】（1）在△ABC中，由已知及余弦定理，比例的性质即可解得BC=3，AB=2，由正弦定理即可解得sin∠ACB的值（2）由（1）及余弦定理可求cos∠ACB，利用两角差的正弦函数公式可求sin∠ACD的值，利用三角形面积公式即可计算得解．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:，以及对余弦定理的定义的理解，了解余弦定理:;;．