题目内容
对于数列{an}若a1=a+(1)求a2、a3、a4,并猜想{an}的表达式;
(2)用数学归纳法证明你的猜想.
解析:(1)∵a1=a+![]() ,
,
an+1=a1-![]() ,
,
∴a2=a1-![]() =a+
=a+![]() -
-![]()
=![]()
a3=a1-![]() =
=![]() .
.
同理可得
a4=![]() .
.
猜想an=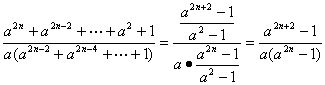 .
.
(2)①当n=1时,右边=![]() =a1,等式成立.
=a1,等式成立.
②假设当n=k时(k∈N*),等式成立,即
ak=![]() ,则当n=k+1时,ak+1=a1-
,则当n=k+1时,ak+1=a1-![]()
![]()
这就是说,当n=k+1时,等式也成立.
根据①②可知,对于一切n∈N*,an=![]() 成立.
成立.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
对于数列{an},若满足a1,
,
,…,
,…是首项为1,公比为2的等比数列,则a100等于( )
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
| A、2100 |
| B、299 |
| C、25050 |
| D、24950 |