题目内容
若点P（x，y）为椭圆
+y2=1上一点，则x+y的最大值为（ ）
| x2 |
| 4 |
分析：先根据条件对其三角换元，再结合三角函数的有界性即可得到结论．
解答：解：因为点P（x，y）为椭圆
+y2=1上一点；
所以可得x=2sinα，y=cosα；
∴x+y=2sinα+cosα=
sin（α+θ），（tanθ=
）；
∵sin（α+θ）∈[-1，1]．
∴x+y的最大值：
．
故选：D．
| x2 |
| 4 |
所以可得x=2sinα，y=cosα；
∴x+y=2sinα+cosα=
| 5 |
| 1 |
| 2 |
∵sin（α+θ）∈[-1，1]．
∴x+y的最大值：
| 5 |
故选：D．
点评：本题主要考查三角换元的应用以及三角函数的有界性，是对知识的综合考查，属于基础题目．
练习册系列答案
阅读快车系列答案
相关题目
+
=1（a＞b＞0）的焦点为F1，F2，P是椭圆上任意一点，若以坐标原点为圆心，椭圆短轴长为直径的圆经过椭圆的焦点，且△PF1F2的周长为4
．
上动点P（x，y）（x-y≠0）处的切线，l与椭圆C交于不同的两点Q，R，证明：∠QOR的大小为定值．
+
=1（a＞b＞0）的焦点为F1，F2，P是椭圆上任意一点，若以坐标原点为圆心，椭圆短轴长为直径的圆经过椭圆的焦点，且△PF1F2的周长为4
．
上动点P（x，y）（x-y≠0）处的切线，l与椭圆C交于不同的两点Q，R，证明：∠QOR的大小为定值．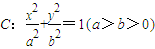
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．