��Ŀ����
��һ��߳�Ϊ4�������θְ�,�ֶ�������и���ӳ�һ��������������(�С�����ĺ��Բ���),����Ӧ����ѧ֪ʶ�����������:��ͼ(1),�ڸְ���ĸ��Ǵ�����ȥһ��С������,ʣ�ಿ��Χ��һ��������,�ó�����ĸ�ΪС�����α߳�,��ͼ(2).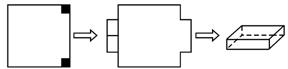
(1)������������и���Ӷ��ɵij����������ݻ�V1;
(2)����������ƴ���ȱ��(���������˷�),������������к�����,ʹ�����˷Ѽ���,�������ó������������ݻ�V2��V1.
�⣺(1)����ȥ�����α߳�Ϊx,�ӳɵij�����ĵ���߳�Ϊ4-2x,��Ϊx,
��V1=(4-2x)2��x=(4x3-16x2+16x)(0��x��2��.
��V1��=4(3x2-8x+4),��V1��=0,��x1=![]() ,x2=2(��ȥ),
,x2=2(��ȥ),
��V1��=12(x-![]() )(x-2),�ֵ�x��
)(x-2),�ֵ�x��![]() ʱ,V1�䣾0;
ʱ,V1�䣾0;
��![]() ��x��2ʱ,V1�䣼0.
��x��2ʱ,V1�䣼0.
�൱x=![]() ʱ,V1ȡ���ֵ
ʱ,V1ȡ���ֵ![]() .
.
(2)������Ʒ�������:
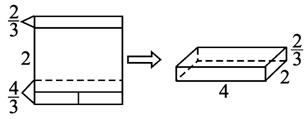
��ͼ��,�������ε������Ǵ�������һ�߳�Ϊ1��С������;��ͼ��,�����µ�С�����κ���δ�пڵ�������һ�ߵ��м�;��ͼ��,��ͼ�ں��ɳ���������.

�� �� ��
�º�����������������һ��������,��Ϊ3,��Ϊ2,�˳������ݻ�V2=3��2��1=6,��ȻV2��V1,�ʵڶ��ַ�������Ҫ��.
���������ͼ��,V3=2��4��![]() =
=![]() ��V1.
��V1.
��
����������������(��).

��ϰ��ϵ�д�
�����Ŀ
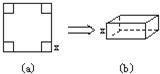 ��һ��߳�Ϊ4�������θְ壬�ֶ�������и���ӳ�һ�������������������С�����ĺ��Բ��ƣ�������Ӧ����ѧ֪ʶ����������ƣ���ͼ��a�����ڸְ���ĸ��Ǵ�����ȥһ��С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ�ΪС�����α߳�����ͼ��b����
��һ��߳�Ϊ4�������θְ壬�ֶ�������и���ӳ�һ�������������������С�����ĺ��Բ��ƣ�������Ӧ����ѧ֪ʶ����������ƣ���ͼ��a�����ڸְ���ĸ��Ǵ�����ȥһ��С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ�ΪС�����α߳�����ͼ��b���� ��2�������ж����������Ƿ�����ѷ����������ǣ������һ���·�����ʹ�����˷����٣������ó������������ݻ�V2��V1.
��2�������ж����������Ƿ�����ѷ����������ǣ������һ���·�����ʹ�����˷����٣������ó������������ݻ�V2��V1. ��
�� ��
��
 ��С�����Σ����ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳���
��С�����Σ����ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳��� ʱ��Vlȡ���ֵ
ʱ��Vlȡ���ֵ ��Ϊ�˲����˷����٣�����ʦ����ʵ�������������ӷ�������д���루1���ĺ��ӷ������ѣ�ʹ�����˷����٣��ݻ���Vl����Ʒ��������������������Ʒ������õ����������ݻ���
��Ϊ�˲����˷����٣�����ʦ����ʵ�������������ӷ�������д���루1���ĺ��ӷ������ѣ�ʹ�����˷����٣��ݻ���Vl����Ʒ��������������������Ʒ������õ����������ݻ���