题目内容
设f(x)=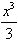 ,对任意实数t,记
,对任意实数t,记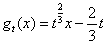 ,
,
(Ⅰ)求函数y=f(x)-gt(x)的单调区间;
(Ⅱ)求证:
(ⅰ)当x>0时,f(x)≥gt(x)对任意正实数t成立;
(ⅱ)有且仅有一个正实数x0,使得gx(x0)≥gt(x0)对任意正实数t成立.
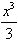 ,对任意实数t,记
,对任意实数t,记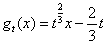 ,
,(Ⅰ)求函数y=f(x)-gt(x)的单调区间;
(Ⅱ)求证:
(ⅰ)当x>0时,f(x)≥gt(x)对任意正实数t成立;
(ⅱ)有且仅有一个正实数x0,使得gx(x0)≥gt(x0)对任意正实数t成立.
(Ⅰ)解: ,
,
由 ,得x=±2,
,得x=±2,
因为当 时,y′>0;当
时,y′>0;当 时,y′<0;当
时,y′<0;当 时,y′>0,
时,y′>0,
故所求函数的单调递增区间是 ,单调递减区间是(-2,2)。
,单调递减区间是(-2,2)。
(Ⅱ)证明:(i)令 ,
,
则 ,
,
当t>0时,由h′(x)=0,得 ,
,
当 时,h′(x)>0,
时,h′(x)>0,
所以h(x)在(0,+∞)内的最小值是 ;
;
故当x>0时, 对任意正实数t成立;
对任意正实数t成立;
(ii) ,
,
由(i)得, 对任意正实数t成立.
对任意正实数t成立.
即存在正实数 ,使得
,使得 对任意正实数t成立.
对任意正实数t成立.
下面证明 的唯一性:
的唯一性:
当 ,t=8时,
,t=8时,
 ,
,
由(i)得, ,
,
再取 ,得
,得 ,
,
所以 ,
,
即 时,不满足
时,不满足 对任意t>0都成立,
对任意t>0都成立,
故有且仅有一个正实数 ,使得
,使得 对任意正实数t成立.
对任意正实数t成立.
 ,
,由
 ,得x=±2,
,得x=±2,因为当
 时,y′>0;当
时,y′>0;当 时,y′<0;当
时,y′<0;当 时,y′>0,
时,y′>0,故所求函数的单调递增区间是
 ,单调递减区间是(-2,2)。
,单调递减区间是(-2,2)。(Ⅱ)证明:(i)令
 ,
,则
 ,
,当t>0时,由h′(x)=0,得
 ,
,当
 时,h′(x)>0,
时,h′(x)>0,所以h(x)在(0,+∞)内的最小值是
 ;
;故当x>0时,
 对任意正实数t成立;
对任意正实数t成立;(ii)
 ,
,由(i)得,
 对任意正实数t成立.
对任意正实数t成立.即存在正实数
 ,使得
,使得 对任意正实数t成立.
对任意正实数t成立.下面证明
 的唯一性:
的唯一性:当
 ,t=8时,
,t=8时, ,
,由(i)得,
 ,
,再取
 ,得
,得 ,
,所以
 ,
,即
 时,不满足
时,不满足 对任意t>0都成立,
对任意t>0都成立,故有且仅有一个正实数
 ,使得
,使得 对任意正实数t成立.
对任意正实数t成立.
练习册系列答案
相关题目