题目内容
（2013•和平区二模）如图，在△ABC的边AB、AC上分别取点M、N，使| AM |
| 1 |
| 3 |
| AB |
| AN |
| 1 |
| 4 |
| AC |
| BP |
| PN |
| PM |
| CP |
| λ |
| μ |
分析：选取
、
为基向量，分别在△ANP、△AMP中利用三角形法则表示出
，根据平面向量基本定理可知表示唯一，从而得到方程组，解出μ、λ，进而得到答案．
| AB |
| AC |
| AP |
解答：解：
=
+
=
+
=
+
(
-
)
=
+
(
-
)
=
+
，
=
+
=
+
=
+
(
-
)
=
+
(
-
)
=
+
，
所以
，解得
，
所以
=12，
故选D．
| AP |
| AN |
| NP |
| 1 |
| 4 |
| AC |
| 1 |
| λ+1 |
| NB |
=
| 1 |
| 4 |
| AC |
| 1 |
| λ+1 |
| AB |
| AN |
=
| 1 |
| 4 |
| AC |
| 1 |
| λ+1 |
| AB |
| 1 |
| 4 |
| AC |
=
| λ |
| 4(λ+1) |
| AC |
| 1 |
| λ+1 |
| AB |
| AP |
| AM |
| MP |
| 1 |
| 3 |
| AB |
| μ |
| μ+1 |
| MC |
=
| 1 |
| 3 |
| AB |
| μ |
| μ+1 |
| AC |
| AM |
=
| 1 |
| 3 |
| AB |
| μ |
| μ+1 |
| AC |
| 1 |
| 3 |
| AB |
=
| μ |
| μ+1 |
| AC |
| 1 |
| 3(μ+1) |
| AB |
所以
|
|
所以
| λ |
| μ |
故选D．
点评：本题考查平面向量基本定理及其意义，考查向量的线性运算，属中档题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
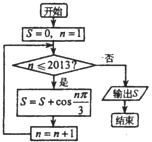（2013•和平区二模）阅读如图所示的程序框图，运行相应的程序，则输出的结果S的值为（ ）
（2013•和平区二模）已知函数y=Asin（ωx+φ）（A＞0，ω＞0），|φ|＜π）的部分图象如图所示，则它的解析式为（ ）