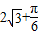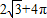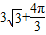题目内容
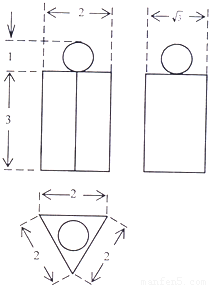
 如图为一个几何体的三视图,主视图和左视图为全等的等腰梯形,上、下底边长分别为2,4.俯视图中内,内外为正方形,边长分别为2,4,几何体的高为3,求此几何体的表面积和体积.
如图为一个几何体的三视图,主视图和左视图为全等的等腰梯形,上、下底边长分别为2,4.俯视图中内,内外为正方形,边长分别为2,4,几何体的高为3,求此几何体的表面积和体积.分析:由几何体的三视图可得几何体是正四棱台,连接BD,B′D′,过B′分别作下底面及BC的垂线交BD于E,BC于F,根据上下底面正方形的边长可得:BE=
,BF=1,再根据几何体的高为3,可得正四棱台的斜高与正四棱台的高,进而根据有关的公式求出几何体的表面积与体积.
| 2 |
解答:解:由几何体的三视图可得几何体是正四棱台,如图所示,

连接BD,B′D′,过B′分别作下底面及BC的垂线交BD于E,BC于F,
因为内外为正方形,边长分别为2,4,
所以BE=
,BF=1,
又因为几何体的高为3,即B′E=3,
所以BB′=
,
所以B'F=
------------(6分)
所以S全面积=20+12
-----(10分)
V台=
(4+
+16)×3=28-----(14分)

连接BD,B′D′,过B′分别作下底面及BC的垂线交BD于E,BC于F,
因为内外为正方形,边长分别为2,4,
所以BE=
| 2 |
又因为几何体的高为3,即B′E=3,
所以BB′=
| 11 |
所以B'F=
| 10 |
所以S全面积=20+12
| 10 |
V台=
| 1 |
| 3 |
| 4×16 |
点评:本题主要借助于几何体的三视图考查几何体的表面积公式与几何体的体积公式,考查了学生的空间想象能力与识图用图的能力,此题属于基础题.

练习册系列答案
相关题目
 (2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )
(2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )