Question

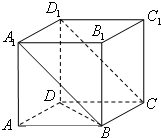（2013•普陀区二模）如图，正方体ABCD-A₁B₁C₁D₁的棱长为1
（1）求直线DB与平面A₁BCD₁所成角的大小；
（2）求四棱锥D-BCD₁A₁的体积．

Answer 1

分析：（1）建立空间直角坐标系，如图所示．利用斜线的方向向量和平面的法向量的夹角即可得到线面角；
（2）利用点到平面的距离公式及四棱锥的体积计算公式即可得出．

解答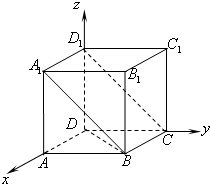：解：（1）以D为坐标原点，分别以射线DA、DC、DD₁为x、y、z轴，建立空间直角坐标系，如图所示．
则D（0，0，0），B（1，1，0），C（0，1，0），D₁（0，0，1）．

DB

=(1，1，0)，

BC

=(-1，0，0)，

CD1

=(0，-1，1)．
设

n

=(x，y，z)是平面A₁BCD₁的法向量，则

n • BC =0 n • CD1 =0

，即

x=0 z-y=0

令z=1，则y=1，x=0，∴

n

=(0，1，1)．
设直线DB与平面A₁BCD₁所成角为θ，则sinθ=|cos＜

n

，

DB

＞|=

| n • DB |

| n | | DB |

=

1

2 × 2

=

1

2

．
由于0≤θ≤

π

2

，∴θ=

π

6

．
即直线DB与平面A₁BCD₁所成角的大小为

π

6

；
（2）由（1）得

n0

=

n

| n |

=(0，

1

2

，

1

2

)．
∴点D到平面A₁BCD₁的距离d=|

n0

•

DB

|=

2

2

．
∵四边形A₁BCD₁是矩形，∴面积S=BC•CD₁=1×

2

=

2

．
∴VD-BCD1A1=

1

3

sh=

1

3

×

2

2

×

2

=

1

3

．

点评：熟练掌握通过建立空间直角坐标系，利用斜线的方向向量和平面的法向量的夹角得到线面角；利用向量表示点到平面的距离公式，四棱锥的体积计算公式是解题的关键．