题目内容
 如图,CP是圆O的切线,P为切点,直线CO交圆O于A,B两点,AD⊥CP,垂足为D.
如图,CP是圆O的切线,P为切点,直线CO交圆O于A,B两点,AD⊥CP,垂足为D.求证:∠DAP=∠BAP.
分析:利用同弧上的圆周角与弦切角相等,推出∠APB=90°,利用AD⊥CP,推出∠DAP=∠BAP.
解答: 证明:因为CP与圆O 相切,所以∠DPA=∠PBA. …2分
证明:因为CP与圆O 相切,所以∠DPA=∠PBA. …2分
因为AB为圆O直径,所以∠APB=90°,
所以∠BAP=90°-∠PBA. …6分
因为AD⊥CP,所以∠DAP=90°-∠DPA,
所以∠DAP=∠BAP.
 证明:因为CP与圆O 相切,所以∠DPA=∠PBA. …2分
证明:因为CP与圆O 相切,所以∠DPA=∠PBA. …2分因为AB为圆O直径,所以∠APB=90°,
所以∠BAP=90°-∠PBA. …6分
因为AD⊥CP,所以∠DAP=90°-∠DPA,
所以∠DAP=∠BAP.
点评:本题考查圆的切线与圆的内接三角形的关系,考查逻辑推理能力.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 (2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为
(2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为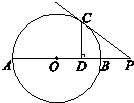 如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.
如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.