题目内容
(本小题满分12分) 已知函数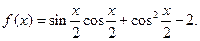
(Ⅰ)将函数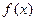 化简成
化简成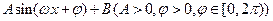 的形式,并指出
的形式,并指出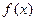 的最小正周期;
的最小正周期;
(Ⅱ)求函数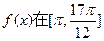 上的最大值和最小值
上的最大值和最小值
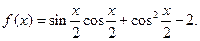
(Ⅰ)将函数
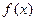 化简成
化简成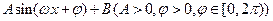 的形式,并指出
的形式,并指出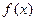 的最小正周期;
的最小正周期;(Ⅱ)求函数
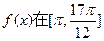 上的最大值和最小值
上的最大值和最小值(Ⅰ)f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)f(x)有最小值-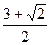 ;f(x)有最大值-2.
;f(x)有最大值-2.
(Ⅱ)f(x)有最小值-
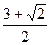 ;f(x)有最大值-2.
;f(x)有最大值-2.解 (Ⅰ) f(x)=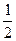 sinx+
sinx+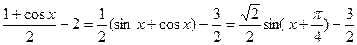 .
.
故f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)由π≤x≤ ,得
,得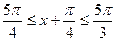 .因为f(x)=
.因为f(x)=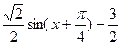 在
在
[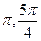 ]上是减函数,在[
]上是减函数,在[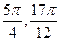 ]上是增函数,故当x=
]上是增函数,故当x=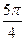 时,f(x)有最小值-
时,f(x)有最小值-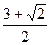 ;而f(π)=-2,f(
;而f(π)=-2,f(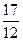 π)=-
π)=-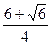 <-2,所以当x=π时,f(x)有最大值-2.
<-2,所以当x=π时,f(x)有最大值-2.
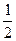 sinx+
sinx+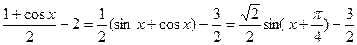 .
.故f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)由π≤x≤
 ,得
,得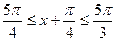 .因为f(x)=
.因为f(x)=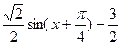 在
在[
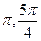 ]上是减函数,在[
]上是减函数,在[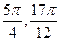 ]上是增函数,故当x=
]上是增函数,故当x=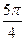 时,f(x)有最小值-
时,f(x)有最小值-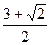 ;而f(π)=-2,f(
;而f(π)=-2,f(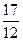 π)=-
π)=-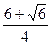 <-2,所以当x=π时,f(x)有最大值-2.
<-2,所以当x=π时,f(x)有最大值-2.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
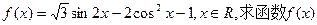 的最小正周期; (II)设
的最小正周期; (II)设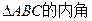 A、B、C的对边分别为a、b、c,且
A、B、C的对边分别为a、b、c,且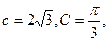 若向量
若向量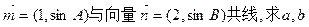 的值。
的值。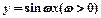 在一个周期内的图象如图所示,要得到函数
在一个周期内的图象如图所示,要得到函数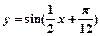 的图象,则需将函数
的图象,则需将函数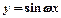 的图象( )
的图象( )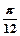
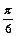
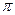 ,且在
,且在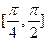 上为减函数的是( )
上为减函数的是( )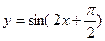
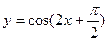
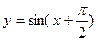
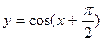
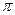 为周期,图象关于直线
为周期,图象关于直线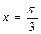 对称的函数是( )
对称的函数是( )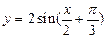

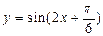

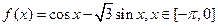 的单调递增区间是
的单调递增区间是



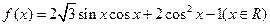
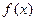 的最小正周期及单调递减区间
的最小正周期及单调递减区间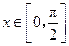 时,求
时,求 x (
x (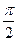 )上是单调函数,则实数
)上是单调函数,则实数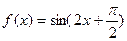 ,
,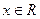 ,则
,则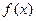 是
是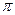 的奇函数 B 最
的奇函数 B 最 小正周期为
小正周期为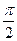 的奇函数
的奇函数