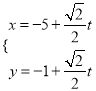题目内容
【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.

(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
【答案】见解析
【解析】解 (1)由∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a,
a,
所以∠BAC=![]() .
.
设MA=MA′=xa(0<x<1),则MB=a-xa,
所以在Rt△MBA′中,cos(π-2θ)=![]() =
=![]() ,
,
所以x=![]() .
.
由于△AMN为等边三角形,
所以绿地的面积
S=2×![]() ×
×![]() a×
a×![]() a×sin
a×sin![]() =
=![]() a2.
a2.
(2)因为在Rt△ABC中,∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a,
a,
所以∠BAC=![]() ,所以在△AMN中,∠ANM=
,所以在△AMN中,∠ANM=![]() -θ,
-θ,
由正弦定理得![]() =
= ,
,
设AM=ax(0<x<1),则A′M=ax,BM=a-ax,
所以在Rt△MBA′中,cos(π-2θ)=![]() =
=![]() ,
,
所以x=![]() ,即AM=
,即AM=![]() ,
,
所以AN=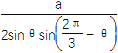 .
.
2sinθsin![]() =sin2θ+
=sin2θ+![]() sinθcosθ
sinθcosθ
=![]() +
+![]() sin2θ-
sin2θ-![]() cos2θ=
cos2θ=![]() +sin(2θ-
+sin(2θ-![]() ),
),
因为![]() <θ<
<θ<![]() ,所以
,所以![]() <2θ-
<2θ-![]() <
<![]() ,
,
所以当且仅当2θ-![]() =
=![]() ,即θ=
,即θ=![]() 时,AN的值最小,且AN=
时,AN的值最小,且AN=![]() a,此时绿地公共走道的长度MN=
a,此时绿地公共走道的长度MN=![]() a.
a.

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:t)和年利润
(单位:t)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
和年销售量![]() (i=1,2,…,8)数据作了初步处理,得到右面的散点图及一些统计量的值.
(i=1,2,…,8)数据作了初步处理,得到右面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
, ![]()
(1)根据散点图判断, ![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
①年宣传费![]() =49时,年销售量及年利润的预报值是多少?
=49时,年销售量及年利润的预报值是多少?
②年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
, ![]() …,
…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
![]()