题目内容
已知函数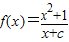 的图象关于原点对称.
的图象关于原点对称.(1)求f(x)的表达式;
(2)n≥2,n∈N时,求证:[f(1)-1]|[f(22)-22]+…+[f(n2)-n2]<2;
(3)对n≥2,n∈N,x>0,求证[f(x)]n-f(xn)≥2n-2.
【答案】分析:(1)用特殊值直接代入,得f(1)=-f(-1),解此方程,即可求得c的值.
(2)利用放缩法,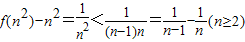 ,再根据列项相消求和即可.
,再根据列项相消求和即可.
(3)利用二项式定理,将[f(x)]n-f(xn)展开,然后根据二项式系数相等的项,合并成n-1对,每一个括号里面都使用基本不等式,可以证出[f(x)]n-f(xn)≥Cn1+Cn2+…+Cnn-1=2n-2,达到证明的目的.
解答:解:∵f(x)图象关于原点对称
∴f(x)是奇函数,代入特值,f(1)=-f(-1),求得c=0
∴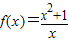
(2)∵n≥2,n∈N
∴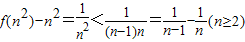
∴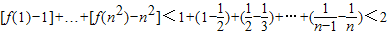
(3)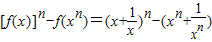
=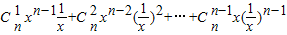
=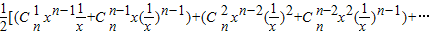
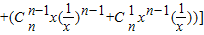
≥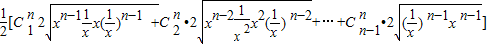 =2n-2
=2n-2
∴[f(x)]n-f(xn)≥2n-2.
点评:本题考查了函数与不等式的综合,二项式定理等等知识点,属于难题.合理地将条件加以运用,适时利用基本不等式,是解决本题的关键、
(2)利用放缩法,
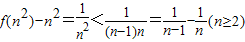 ,再根据列项相消求和即可.
,再根据列项相消求和即可.(3)利用二项式定理,将[f(x)]n-f(xn)展开,然后根据二项式系数相等的项,合并成n-1对,每一个括号里面都使用基本不等式,可以证出[f(x)]n-f(xn)≥Cn1+Cn2+…+Cnn-1=2n-2,达到证明的目的.
解答:解:∵f(x)图象关于原点对称
∴f(x)是奇函数,代入特值,f(1)=-f(-1),求得c=0
∴
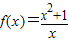
(2)∵n≥2,n∈N
∴
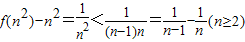
∴
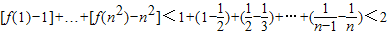
(3)
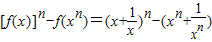
=
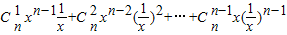
=
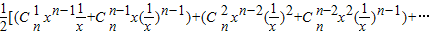
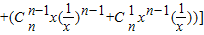
≥
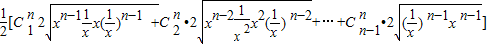 =2n-2
=2n-2∴[f(x)]n-f(xn)≥2n-2.
点评:本题考查了函数与不等式的综合,二项式定理等等知识点,属于难题.合理地将条件加以运用,适时利用基本不等式,是解决本题的关键、

练习册系列答案
相关题目
 ,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来)
,∠B=60°,AB=1的△ABC有两个.其中正确命题的代号是_________.(按照原顺序将所有正确命题的代号都写出来) ,给出下列命题:
,给出下列命题:
 ,则f(x)在区间[a,+∞)上是增函数;
,则f(x)在区间[a,+∞)上是增函数; ,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).
,其中正确命题的代号是________(按照原顺序将你认为正确的命题的代号都填上).