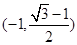题目内容
函数 的值域是
的值域是
- A.[-1,3]
- B.[-1,4]
- C.(-6,3]
- D.(-2,4]
C
分析:利用二倍角公式化简函数的解析式为y=-16 +3,根据0<sinx<1,再利用二次函数的性质可得函数y的值域.
+3,根据0<sinx<1,再利用二次函数的性质可得函数y的值域.
解答:∵函数 =
= -
-
=3-4sin2x-
=3-4sin2x-4cos2x cos2x+3cos2x+2sin3xsinx
=3-4sin2x-4(1-sin2x)(1-2sin2x)+3(1-2sin2x)+2(3sinx-4sin3x)sinx
=2+8sin2x-16sin4x=-16 +3,且 0<x
+3,且 0<x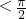 ,∴0<sinx<1,
,∴0<sinx<1,
∴当 sinx= 时,函数取得最大值为 3,当 sinx 趋于1 时,函数的最小值趋于-6,
时,函数取得最大值为 3,当 sinx 趋于1 时,函数的最小值趋于-6,
即函数的值域为 (-6,3],
故选 C.
点评:本题主要考查二倍角公式、正弦函数的定义域和值域,二次函数的性质应用,属于中档题.
分析:利用二倍角公式化简函数的解析式为y=-16
 +3,根据0<sinx<1,再利用二次函数的性质可得函数y的值域.
+3,根据0<sinx<1,再利用二次函数的性质可得函数y的值域.解答:∵函数
 =
= -
-
=3-4sin2x-

=3-4sin2x-4cos2x cos2x+3cos2x+2sin3xsinx
=3-4sin2x-4(1-sin2x)(1-2sin2x)+3(1-2sin2x)+2(3sinx-4sin3x)sinx
=2+8sin2x-16sin4x=-16
 +3,且 0<x
+3,且 0<x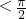 ,∴0<sinx<1,
,∴0<sinx<1,∴当 sinx=
 时,函数取得最大值为 3,当 sinx 趋于1 时,函数的最小值趋于-6,
时,函数取得最大值为 3,当 sinx 趋于1 时,函数的最小值趋于-6,即函数的值域为 (-6,3],
故选 C.
点评:本题主要考查二倍角公式、正弦函数的定义域和值域,二次函数的性质应用,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,则函数
,则函数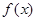 的值域是( ).
的值域是( ).  B.
B.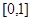 C.
C.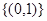 D.
D.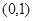
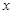 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数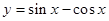 的值域是( )
的值域是( ) B.
B.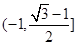 C.
C.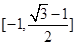 D.
D.