题目内容
下列函数中,在其定义域上是减函数的是( )
| A、f(x)=-x2+x+1 | ||
B、f(x)=
| ||
C、f(x)=(
| ||
| D、f(x)=ln(2-x) |
分析:f(x)=-x2+x+1在其定义域上先增后减;f(x)=
在(-∞,0)和(0,+∞)上都是减函数,但是在其整个定义域上没有单调性;当x≤0时,f(x)=(
)|x|是增函数;f(x)=ln(2-x)在其定义域上是减函数.
| 1 |
| x |
| 1 |
| 3 |
解答:解:f(x)=-x2+x+1在其定义域上先增后减,故A不成立;
f(x)=
在(-∞,0)和(0,+∞)上都是减函数,但是在其整个定义域上没有单调性,故B不成立;
当x≤0时,f(x)=(
)|x|是增函数,故C不成立;
f(x)=ln(2-x)在其定义域上是减函数,故D成立.
f(x)=
| 1 |
| x |
当x≤0时,f(x)=(
| 1 |
| 3 |
f(x)=ln(2-x)在其定义域上是减函数,故D成立.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
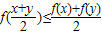 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数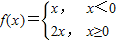
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数