题目内容
在△ABC中，三个内角A，B，C所对的边为a，b，c，且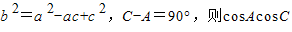
=（ ）A．
B．-
C．
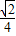
D．-
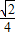
【答案】分析：根据余弦定理，结合已知条件边的平方关系可得B=60°，再由三角形内角和定理结合C-A=90°，解得A=15°，C=105°．由此结合特殊角的三角函数值及和与差的余弦公式公式，不难算出cosAcosC的值．
解答：解：∵在△ABC中，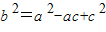
∴cosB=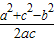
=
=
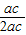结合B∈（0°，180°），得B=60°
∵C-A=90°，C+A=180°-B=120°
∴C=105°，A=15°，
得cosA=cos（45°-30°）=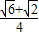
，cosC=cos（45°++60°）=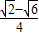
∴cosAcosC=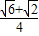
•
=-
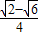故选：B
点评：本题在△ABC中，已知边的平方关系和两角之差，求两个角的余弦之积，着重考查了运用余弦定理解三角形、两角和与差的余弦公式和特殊角的三角函数值等知识，属于基础题．
解答：解：∵在△ABC中，
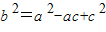
∴cosB=
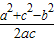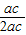==结合B∈（0°，180°），得B=60°
∵C-A=90°，C+A=180°-B=120°
∴C=105°，A=15°，
得cosA=cos（45°-30°）=
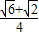，cosC=cos（45°++60°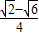）=∴cosAcosC=
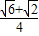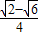•=-故选：B
点评：本题在△ABC中，已知边的平方关系和两角之差，求两个角的余弦之积，着重考查了运用余弦定理解三角形、两角和与差的余弦公式和特殊角的三角函数值等知识，属于基础题．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
相关题目