题目内容
函数 的单调递减区间是
的单调递减区间是
- A.
 (k∈Z)
(k∈Z) - B.
 (k∈Z)
(k∈Z) - C.
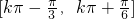 (k∈Z)
(k∈Z) - D.
 (k∈Z)
(k∈Z)
D
分析:通过对数的真数大于0,结合正弦函数的单调减区间,求出函数的单调减区间即可.
解答:由题意可知 ,
,
函数的单调减区间满足 ,
,
所以 ,
,
解得 ,
,
即x∈ ,k∈Z.
,k∈Z.
故选D.
点评:本题考查复合函数的单调性,三角函数的单调性,考查函数与方程的思想,计算能力.
分析:通过对数的真数大于0,结合正弦函数的单调减区间,求出函数的单调减区间即可.
解答:由题意可知
 ,
,函数的单调减区间满足
 ,
,所以
 ,
,解得
 ,
,即x∈
 ,k∈Z.
,k∈Z.故选D.
点评:本题考查复合函数的单调性,三角函数的单调性,考查函数与方程的思想,计算能力.

练习册系列答案
相关题目

 的单调递减区间是 .
的单调递减区间是 .  的单调递减区间是 . (科网
的单调递减区间是 . (科网