题目内容
下列结论正确的是（ ）A．?x∈R，使2x2-x+1＜0成立
B．?x＞0，都有
成立C．函数
的最小值为2D．0＜x≤2时，函数y=x-
有最大值为
【答案】分析：2x2-x+1=2
+
＞0，x≤0时，B不成立，
的最小值大于2，0＜x≤2时，函数D：y=x-
有最大值为
，成立．
解答：解：∵2x2-x+1=2
+
＞0，故A不成立；
当x≤0时，B不成立；
函数
的最小值大于2，故C不成立；
0＜x≤2时，函数y=x-
有最大值为
，D成立．
故选D．
点评：本题考查基本不等式的性质和应用，解题时要注意均值不等式的合理运用．
+＞0，x≤0时，B不成立，的最小值大于2，0＜x≤2时，函数D：y=x-有最大值为，成立．解答：解：∵2x2-x+1=2
+＞0，故A不成立；当x≤0时，B不成立；
函数
的最小值大于2，故C不成立；0＜x≤2时，函数y=x-
有最大值为，D成立．故选D．
点评：本题考查基本不等式的性质和应用，解题时要注意均值不等式的合理运用．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
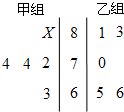如图所示茎叶图记录了甲乙两组各5名同学的数学成绩．甲组成绩中有一个数据模糊，无法确认，在图中以X表示．若两个小组的平均成绩相同，则下列结论正确的是（ ）| A、X=2，S甲2＜S乙2 | B、X=2，S甲2＞S乙2 | C、X=6，S甲2＜S乙2 | D、X=6，2，S甲2＞S乙2 |