题目内容
已知向量 与向量
与向量 共线,且满足
共线,且满足 ,
, ,则
,则 = ,k= .
= ,k= .
【答案】分析:本题考查的知识点是空间向量的共线与垂直及数量积运算,我们要求向量 ,我们可以根据向量
,我们可以根据向量 与向量
与向量 共线,且满足
共线,且满足 ,结合向量共线的性质,构造方程进行解答,再由
,结合向量共线的性质,构造方程进行解答,再由 结合向量垂直的性质,构造关于K的方程,解方程即可求出K值.
结合向量垂直的性质,构造关于K的方程,解方程即可求出K值.
解答:解:∵向量 与向量
与向量 共线,
共线,
且 ,
,
∴向量 与向量
与向量 同向
同向
设 ,则
,则 =
=
解得:λ=2
则 =(4,-2,4)
=(4,-2,4)
若
则
= =0
=0
解得:k=±2
故答案为:(4,-2,4),±2
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数.如果两个向量垂直,则它们的夹角为 ,此时向量的数量积,等于0.判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.
,此时向量的数量积,等于0.判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.
 ,我们可以根据向量
,我们可以根据向量 与向量
与向量 共线,且满足
共线,且满足 ,结合向量共线的性质,构造方程进行解答,再由
,结合向量共线的性质,构造方程进行解答,再由 结合向量垂直的性质,构造关于K的方程,解方程即可求出K值.
结合向量垂直的性质,构造关于K的方程,解方程即可求出K值.解答:解:∵向量
 与向量
与向量 共线,
共线,且
 ,
,∴向量
 与向量
与向量 同向
同向设
 ,则
,则 =
=
解得:λ=2
则
 =(4,-2,4)
=(4,-2,4)若

则

=
 =0
=0解得:k=±2
故答案为:(4,-2,4),±2
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数.如果两个向量垂直,则它们的夹角为
 ,此时向量的数量积,等于0.判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”.
,此时向量的数量积,等于0.判断两个向量的关系(平行或垂直)或是已知两个向量的关系求未知参数的值,要熟练掌握向量平行(共线)及垂直的坐标运算法则,即“两个向量若平行,交叉相乘差为0,两个向量若垂直,对应相乘和为0”. 
练习册系列答案
相关题目

 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值;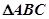 的内角
的内角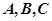 的对应边分别为
的对应边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值.
的值.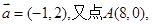
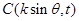
 与向量
与向量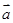 共线。
共线。 取最大值为4时,求
取最大值为4时,求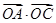 的值。
的值。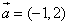 ,点A(8,0),B(n,t),
,点A(8,0),B(n,t),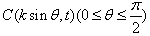 。
。 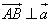 ,且
,且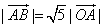 ,求向量
,求向量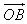 ;
;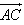 与向量
与向量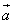 共线,当k>4时,tsinθ的最大值为4,求
共线,当k>4时,tsinθ的最大值为4,求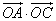 的值。
的值。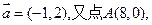
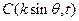
 与向量
与向量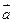 共线。
共线。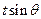 取最大值为4时,求
取最大值为4时,求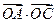 的值。
的值。