题目内容
设z∈C，且|z+1|-|z-i|=0，则|z+i|的最小值为分析：根据题意，可得满足|z+1|-|z-i|=0的点Z几何意义为复平面内的点到（-1，0）与（0，1）的中垂直平分线，进而分析|z+i|的几何意义，可得答案．
解答：解：根据题意，可得满足|z+1|-|z-i|=0的点Z几何意义为复平面内的点到（-1，0）与（0，1）的垂直平分线：x+y=0，
|z+i|的最小值，就是直线上的点与（0，-1）距离的最小值：
=
．
故答案为：
．
|z+i|的最小值，就是直线上的点与（0，-1）距离的最小值：
| |1| | ||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题是基础题，考查复数的模的基本运算，复数模的几何意义，点到直线的距离的求法，考查计算能力．
练习册系列答案
一本好题口算题卡系列答案
相关题目
设z∈C，且|z|=1，当|（z-1）（z-i）|最大时，z=（ ）
| A、-1 | ||||||||
| B、-i | ||||||||
C、-
| ||||||||
D、
|
-
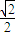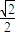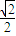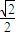i
+
i
