题目内容
(理科做:)已知A(1,1)是椭圆
+
=1 (a>b>0)上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4.
(I)求两焦点的坐标;
(II)设点C、D是椭圆上的两点,直线AC、AD的倾斜角互补,直线CD的斜率是否为定值?若是定值,求出其值;若不是定值,则说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(I)求两焦点的坐标;
(II)设点C、D是椭圆上的两点,直线AC、AD的倾斜角互补,直线CD的斜率是否为定值?若是定值,求出其值;若不是定值,则说明理由.
分析:(I)由|AF1|+|AF2|=4,知a=2,设椭圆方程为
+
=1,把(1,1)代入,得
+
=1,得b2=
,由此能求出两焦点的坐标.
(II)设AC:y=k(x-1)+1,联立
,得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0,由A(1,1)在椭圆上,方程有一个根为xA=1,知xC=
,由AC与AD的倾斜角互补,能推导出CD的斜率为定值.
| x2 |
| 4 |
| y2 |
| b2 |
| 1 |
| 4 |
| 1 |
| b2 |
| 4 |
| 3 |
(II)设AC:y=k(x-1)+1,联立
|
| 3k2-6k-1 |
| 3k2+1 |
解答:解:(I)∵|AF1|+|AF2|=4,
∴2a=4,∴a=2,
设椭圆方程为
+
=1,
把(1,1)代入,得
+
=1,
∴b2=
,
∴c2=4-
=
,
∴两焦点的坐标F1(-
,0),F2(
,0).
(II)设AC:y=k(x-1)+1,
联立
,
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0,
∵A(1,1)在椭圆上,方程有一个根为xA=1,
∴xC=
,
∵AC与AD的倾斜角互补,
∴AD为:y=-k(x-1)+1,
同理,xD=
,
∵yC=k(xC-1)+1,
yD=-k(xD-1)+1,
yC-yD=k(xC+xD)-2k,
∴kCD=
=
.
故CD的斜率为定值
.
∴2a=4,∴a=2,
设椭圆方程为
| x2 |
| 4 |
| y2 |
| b2 |
把(1,1)代入,得
| 1 |
| 4 |
| 1 |
| b2 |
∴b2=
| 4 |
| 3 |
∴c2=4-
| 4 |
| 3 |
| 8 |
| 3 |
∴两焦点的坐标F1(-
2
| ||
| 3 |
2
| ||
| 3 |
(II)设AC:y=k(x-1)+1,
联立
|
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0,
∵A(1,1)在椭圆上,方程有一个根为xA=1,
∴xC=
| 3k2-6k-1 |
| 3k2+1 |
∵AC与AD的倾斜角互补,
∴AD为:y=-k(x-1)+1,
同理,xD=
| 3k2+6k-1 |
| 3k2+1 |
∵yC=k(xC-1)+1,
yD=-k(xD-1)+1,
yC-yD=k(xC+xD)-2k,
∴kCD=
| yC-yD |
| xC-xD |
| 1 |
| 3 |
故CD的斜率为定值
| 1 |
| 3 |
点评:本题考查直线与椭圆的位置关系,考查运算求解能力,考查论证推导能力,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
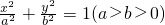 上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4.
上一点,F1、F2是椭圆的两个焦点,且满足|AF1|+|AF2|=4.