题目内容
点P在椭圆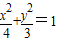 上运动,Q、R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的取值范围为 .
上运动,Q、R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的取值范围为 .
【答案】分析:椭圆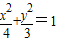 的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.设椭圆左右焦点为F1,F2,由三角形两边之差小于第三边知:|PQ|最小为|PF1|-1,最大为|PF1|+1,同理:|PR|最小为|PF2|-1,最大为|PF2|+1,从而可求|PQ|+|PR|的取值范围.
的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.设椭圆左右焦点为F1,F2,由三角形两边之差小于第三边知:|PQ|最小为|PF1|-1,最大为|PF1|+1,同理:|PR|最小为|PF2|-1,最大为|PF2|+1,从而可求|PQ|+|PR|的取值范围.
解答:解:椭圆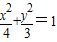 的两焦点为(-1,0),(1,0),恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.
的两焦点为(-1,0),(1,0),恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.
设椭圆左右焦点为F1,F2,由三角形两边之差小于第三边知:|PQ|最小为|PF1|-1,最大为|PF1|+1
同理:|PR|最小为|PF2|-1,最大为|PF2|+1
∴|PQ|+|PR|的最小为|PF1|+|PF2|-2=2×2-2=2,最大为|PF1|+|PF2|+2=2×2+2=6
故|PQ|+|PR|的取值范围为[2,6]
故答案为:[2,6]
点评:本题的考点是圆与圆锥曲线的综合,考查线段和的取值范围问题,解题的关键是利用椭圆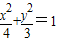 的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.
的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.
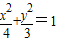 的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.设椭圆左右焦点为F1,F2,由三角形两边之差小于第三边知:|PQ|最小为|PF1|-1,最大为|PF1|+1,同理:|PR|最小为|PF2|-1,最大为|PF2|+1,从而可求|PQ|+|PR|的取值范围.
的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.设椭圆左右焦点为F1,F2,由三角形两边之差小于第三边知:|PQ|最小为|PF1|-1,最大为|PF1|+1,同理:|PR|最小为|PF2|-1,最大为|PF2|+1,从而可求|PQ|+|PR|的取值范围.解答:解:椭圆
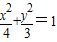 的两焦点为(-1,0),(1,0),恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.
的两焦点为(-1,0),(1,0),恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.设椭圆左右焦点为F1,F2,由三角形两边之差小于第三边知:|PQ|最小为|PF1|-1,最大为|PF1|+1
同理:|PR|最小为|PF2|-1,最大为|PF2|+1
∴|PQ|+|PR|的最小为|PF1|+|PF2|-2=2×2-2=2,最大为|PF1|+|PF2|+2=2×2+2=6
故|PQ|+|PR|的取值范围为[2,6]
故答案为:[2,6]
点评:本题的考点是圆与圆锥曲线的综合,考查线段和的取值范围问题,解题的关键是利用椭圆
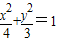 的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标.
的两焦点恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心坐标. 
练习册系列答案
相关题目
 上运动,Q、R分别在两圆
上运动,Q、R分别在两圆 和
和 上运动,则
上运动,则 的最大值为( )
的最大值为( )
 上运动,Q、R分别在两圆
上运动,Q、R分别在两圆 和
和 上运动,则
上运动,则 的最大值为(
)
的最大值为(
) 上运动,Q、R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的最大值为( )
上运动,Q、R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的最大值为( ) 上运动,Q、R分别在两圆
上运动,Q、R分别在两圆 和
和 上运动,则
上运动,则 的最大值为
;最小值为
.
的最大值为
;最小值为
.