题目内容
根据下列条件求圆锥曲线的标准方程.
( I)焦点在x轴上,实轴长是10,虚轴长是8的双曲线方程;
( II)经过两点P1(
,1),P2(-
,-
)的椭圆.
( I)焦点在x轴上,实轴长是10,虚轴长是8的双曲线方程;
( II)经过两点P1(
| 6 |
| 3 |
| 2 |
分析:(I)由双曲线的焦点在x轴上,实轴长是10,虚轴长是8,求出a,b值,代入可得双曲线方程
(II)设椭圆方程为mx2+ny2=1,(m>0,n>0),代入两定点坐标,构造关于m,n的方程,求出m,n值可得椭圆的方程.
(II)设椭圆方程为mx2+ny2=1,(m>0,n>0),代入两定点坐标,构造关于m,n的方程,求出m,n值可得椭圆的方程.
解答:解:( I)∵双曲线的焦点在x轴上,实轴长是10,虚轴长是8
故a=5,b=4
则a2=25,b2=16
故双曲线方程为
-
=1
(II)设椭圆方程为mx2+ny2=1,(m>0,n>0)
由椭圆经过两点P1(
,1),P2(-
,-
)两点
则
解得
故椭圆方程为
+
=1
故a=5,b=4
则a2=25,b2=16
故双曲线方程为
| x2 |
| 25 |
| y2 |
| 16 |
(II)设椭圆方程为mx2+ny2=1,(m>0,n>0)
由椭圆经过两点P1(
| 6 |
| 3 |
| 2 |
则
|
解得
|
故椭圆方程为
| x2 |
| 9 |
| y2 |
| 3 |
点评:本题考查的知识点是双曲线的标准方程,椭圆的标准方程,(I)的关键是求出a,b的值,(II)中不知道焦点位置,故可用“模糊设法”,将方程设为mx2+ny2=1,(m>0,n>0).

练习册系列答案
相关题目
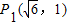 ,
,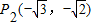 的椭圆.
的椭圆.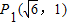 ,
,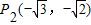 的椭圆.
的椭圆.