题目内容
【题目】已知
.
（1）证明
在
上为增函数；
（2）当
时，解不等式
；
（3）若
在
上恒成立，求
的最大整数值.
【答案】（1）见解析（2）
（3）0
【解析】试题分析：
(1)首先求得函数的导函数，然后对
进行二次求导可得
在
上为增函数；
(2)利用(1)中函数的单调性结合题意可得不等式的解集为
(3)不等式即
，构造新函数
，结合导函数的性质可得
的最大整数值为0.
试题解析：
解：（1）
，设
， 
，
， 
，
|
|
|
|
| - | 0 | + |
| ↓ | 极小值 | ↑ |
，
， 
，
在
上为增函数.
（2）
时， 
， 
在
上为增函数，
若
，则
，与
矛盾；
若
，则
， 
成立.
经化简
，则
， 
，即
，
，即
，
设
，
，
在
上为增函数， 
，得
，
原不等式解集为
.
（3）
在
上为增函数， 
，即
，令
， 
，
设
， 
，
时， 
， 
，
在
为增函数，
在
为增函数，
， 
，
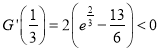有任一解，设为
，
时，
|
|
|
|
| - | 0 | + |
| ↓ | 极 | ↑ |
，
即
，
，
又
， 
.
练习册系列答案
相关题目
