题目内容
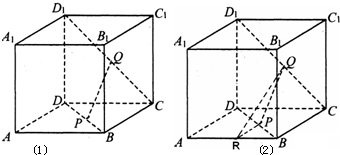已知正方体ABCD-A1B1C1D1中，P、Q分别为对角线BD、CD1上的点，且| CQ |
| QD1 |
| BP |
| PD |
| 2 |
| 3 |
（Ⅰ）求证PQ∥平面A1D1DA；
（Ⅱ）若R是AB上的点，当
| AR |
| AB |
分析：（Ⅰ）连结CP并延长与DA的延长线交于M点，证明BC∥AD，PQ∥MD1，又MD1?平面A1D1DA，PQ?平面A1D1DA，证明PQ∥平面A1D1DA；
（Ⅱ）R是AB上的点，当
的值为
时，能使平面PQR∥平面A1D1DA，通过证明PR∥平面A1D1DA，又PQ∩PR=P，PQ∥平面A1D1DA．然后证明即可．
（Ⅱ）R是AB上的点，当
| AR |
| AB |
| 3 |
| 5 |
解答：（Ⅰ）证明：连结CP并延长与DA的延长线交于M点，
因为四边形ABCD为正方形，所以BC∥AD，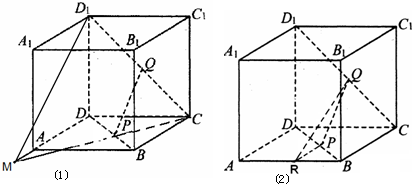
故△PBC∽△PDM，所以
=
=
，
又因为
=
=
，所以
=
=
，所以PQ∥MD1．
又MD1?平面A1D1DA，PQ?平面A1D1DA，故PQ∥平面A1D1DA． …（6分）
（Ⅱ）当
的值为
时，能使平面PQR∥平面A1D1DA．
证明：因为
=
，即有
=
，故
=
，所以PR∥DA．
又DA?平面A1D1DA，PR?平面A1D1DA，
所以PR∥平面A1D1DA，又PQ∩PR=P，PQ∥平面A1D1DA．
所以平面PQR∥平面A1D1DA．…（12分）
因为四边形ABCD为正方形，所以BC∥AD，
故△PBC∽△PDM，所以
| CP |
| PM |
| BP |
| PD |
| 2 |
| 3 |
又因为
| CQ |
| QD1 |
| BP |
| PD |
| 2 |
| 3 |
| CQ |
| QD1 |
| CP |
| PM |
| 2 |
| 3 |
又MD1?平面A1D1DA，PQ?平面A1D1DA，故PQ∥平面A1D1DA． …（6分）
（Ⅱ）当
| AR |
| AB |
| 3 |
| 5 |
证明：因为
| AR |
| AB |
| 3 |
| 5 |
| BR |
| RA |
| 2 |
| 3 |
| BR |
| RA |
| BP |
| PD |
又DA?平面A1D1DA，PR?平面A1D1DA，
所以PR∥平面A1D1DA，又PQ∩PR=P，PQ∥平面A1D1DA．
所以平面PQR∥平面A1D1DA．…（12分）
点评：本题考查直线与平面平行的判定定理，平面与平面平行的判定定理，考查空间想象能力逻辑推理能力．
练习册系列答案
相关题目
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点P在平面DD1C1C内，PD1=PC1=
已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．