题目内容
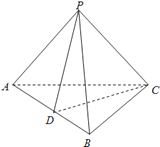
【题目】如图，在四棱锥
中，底面ABCD为梯形，AB//CD，
，AB=AD=2CD=2，△ADP为等边三角形．
(1)当PB长为多少时，平面
平面ABCD?并说明理由；
(2)若二面角
大小为150°，求直线AB与平面PBC所成角的正弦值．
【答案】（1）当
时，平面
平面
，详见解析（2）
【解析】
(1)根据平面和平面垂直可得线面垂直，从而可得
,利用直角三角形知识可得
的长；
(2)构建空间直角坐标系，利用法向量求解直线AB与平面PBC所成角的正弦值.
解：（1）当时，平面平面，
证明如下：在
中，因为
，所以，
又
，
，所以
平面
，
又
平面，所以平面平面；
（2）分别取线段
的中点
，连接
，因为
为等边三角形，
为
的中点，所以
，为的中点，所以
,
又，所以
，故
为二面角
的平面角，所以
，
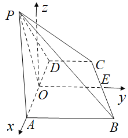
如图，分别以
的方向以及垂直于平面向上的方向作为
轴的正方向，建立空间直角坐标系
，
因为
，，所以
，
，
，
.
可得
，
，
设
为平面
的一个法向量，则有
，
即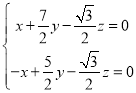
，令
，
可得
，
设
与平面所成角为
，则有
所以直线与平面所成角的正弦值为.
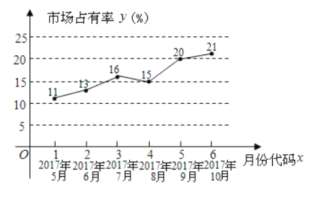
【题目】在2018、2019每高考数学全国Ⅰ卷中，第22题考查坐标系和参数方程，第23题考查不等式选讲.2018年髙考结束后，某校经统计发现:选择第22题的考生较多并且得分率也较高.为研究2019年选做题得分情况，该校高三质量检测的命题完全采用2019年高考选做题模式，在测试结束后，该校数学教师对全校高三学生的选做题得分进行抽样统计，得到两题得分的统计表如下(已知每名学生只选做—道题):
第22题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 50 | 75 | 125 | 200 |
文科人数 | 25 | 25 | 125 | 0 | 25 |
第23题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 30 | 52 | 58 | 60 | 200 |
文科人数 | 5 | 10 | 10 | 5 | 70 |
(1)完成如下2×2列联表，并判断能否有99%的把握认为“选做题的选择”与“文、理科的科类”有关；
选做22题 | 选做23题 | 总计 | |
理科人数 | |||
文科人数 | |||
总计 |
(2)若以全体高三学生选题的平均得分作为决策依据，如果你是考生，根据上面统计数据，你会选做哪道题，并说明理由.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
