题目内容
（本小题满分8分）设函数
的图象在
处的切线方程为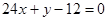
.
（Ⅰ）求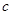
，
；
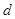（Ⅱ）若函数在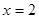
处取得极值
，试求函数解析式并确定函数的单调区间.
【答案】
解：（Ⅰ）
的定义域为
，
，∴
；
-----------------1分
∵切线
的斜率为
，∴
； -----------------2分
把
代入得
，∴P(0,12)，
-----------------3分
∴
.
∴，.
-----------------4分
（Ⅱ）由（Ⅰ）
由已知得：
∴
-----------------5分
∴
∴
-----------------6分
由
得，
；
由
得，
；
-----------------7分
∴的单调增区间为
；
单调减区间为
.
-----------------8分
【解析】略
练习册系列答案
名校课堂系列答案
相关题目
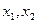是关于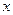
的一元二次方程
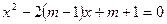的两个实根，又
。
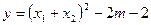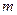的取值范围；
的解析式及最小值。
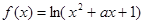的定义域为
.
，
，求实数
的范围；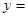
的定义域为
，求实数