题目内容
 (2012•台州一模)函数y=Asin(
(2012•台州一模)函数y=Asin(| π | 2 |
一个最高点,M,N是图象与x轴的交点,若tan∠MPN=-2,则A=
1
1
.分析:依题意,可求得y=Asin(
x+φ)(A>0,φ>0)的周期T=4=MN,设点P在x轴上的射影为Q,tan∠MPQ=
,tan∠NPQ=
,利用∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,即可求得A.
| π |
| 2 |
| 1 |
| A |
| 3 |
| A |
解答:解:∵y=Asin(
x+φ)的周期T=
=4,由图知,MN=T=4,
又P是图象的一个最高点,设点P在x轴上的射影为Q,则MQ=
T=1,QN=
T=3,
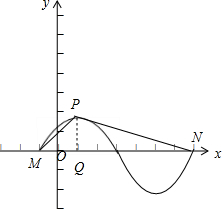
∴tan∠MPQ=
,tan∠NPQ=
,
∵∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,
∴tan(∠MPQ+∠NPQ)=
=
=-2,
∴
-
-1=0,即(
-1)(
+1)=0,又A>0,
∴
=1,A=1.
故答案为:1.
| π |
| 2 |
| 2π | ||
|
又P是图象的一个最高点,设点P在x轴上的射影为Q,则MQ=
| 1 |
| 4 |
| 3 |
| 4 |
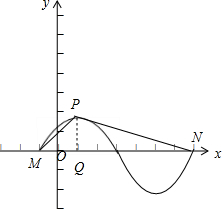
∴tan∠MPQ=
| 1 |
| A |
| 3 |
| A |
∵∠MPQ+∠NPQ=∠MPN,tan∠MPN=-2,
∴tan(∠MPQ+∠NPQ)=
| tan∠MPQ+tan∠NPQ |
| 1-tan∠MPQ•tan∠NPQ |
| ||||
1-
|
∴
| 3 |
| A2 |
| 2 |
| A |
| 1 |
| A |
| 3 |
| A |
∴
| 1 |
| A |
故答案为:1.
点评:本题考查y=Asin(ωx+φ)的图象与性质,考查两角和的正切,考查正弦函数的周期与最值的应用,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目