题目内容
19.某产品整箱出售,每一箱中20件产品,若各箱中次品数为0件,1件,2件的概率分别为80%,10%,10%,现在从中任取-箱,顾客随意抽查4件,如果无次品,则买下该箱产品,如果有次品,则退货.(1)求顾客买下该箱产品的概率;
(2)求在顾客买下的一箱产品中,确实无次品的概率.
分析 (1)设A表示“顾客买下该箱产品”,Bi(i=0,1,2)分别表示“中次品数为0件,1件,2件”,由全概率公式得:P(A)=$\sum _{i=0}^{2}$P(A|Bi)P(Bi),代入计算可得答案.
(2)由贝叶斯公式得:P(B0|A)=P(A|B0)•P(B0)÷P(A),代入可得答案.
解答 解:(1)设A表示“顾客买下该箱产品”,Bi(i=0,1,2)分别表示“中次品数为0件,1件,2件”,
则由已知可得:P(B0)=80%=$\frac{4}{5}$,P(B1)=10%=$\frac{1}{10}$,P(B2)=10%=$\frac{1}{10}$,
则P(A|B0)=1,P(A|B1)=$\frac{{C}_{19}^{4}}{{C}_{20}^{4}}$=$\frac{4}{5}$,P(A|B2)=$\frac{{C}_{18}^{4}}{{C}_{20}^{4}}$=$\frac{12}{19}$.
由全概率公式得:P(A)=$\sum _{i=0}^{2}$P(A|Bi)P(Bi)=$\frac{4}{5}$+$\frac{4}{5}$×$\frac{1}{10}$+$\frac{12}{19}$×$\frac{1}{10}$=$\frac{448}{475}$
(2)由贝叶斯公式得:P(B0|A)=P(A|B0)•P(B0)÷P(A)=$\frac{4}{5}$÷$\frac{448}{475}$=$\frac{95}{112}$
点评 本题考查的知识点是全概率公式和贝叶斯公式,是高等数学概率的拓展,难度较大.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
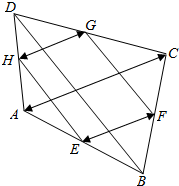 如图,E,F,G,H分别是四边形ABCD的各边中点,分别指出图中:
如图,E,F,G,H分别是四边形ABCD的各边中点,分别指出图中: