题目内容
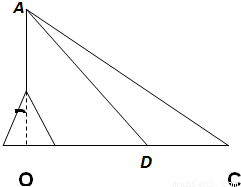
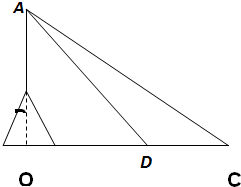如图，某海域内的岛屿上有一直立信号塔AB，设AB延长线与海平面交于点O．测量船在点O的正东方向点C处，测得塔顶A的仰角为30°，然后测量船沿CO方向航行至D处，当CD=100（| 3 |
（1）求信号塔顶A到海平面的距离AO；
（2）已知AB=52米，测量船在沿CO方向航行的过程中，设DO=x，则当x为何值时，使得在点D处观测信号塔AB的视角∠ADB最大．
分析：（1）由题意知，在△ACD中，∠ACD=30°，∠DAC=15°，利用正弦定理可求得AD，在直角△AOD中，∠ADO=45°，从而可求得AO；
（2）设∠ADO=α，∠BDO=β，依题意，tanα=
，tanβ=
，可求得tan∠ADB=tan（α-β）=
=
，利用基本不等式可求得tan∠ADB的最大值，从而可得答案．
（2）设∠ADO=α，∠BDO=β，依题意，tanα=
| 100 |
| x |
| 48 |
| x |
| 52x |
| x2+4800 |
| 52 | ||
x+
|
解答：解：（1）由题意知，在△ACD中，∠ACD=30°，∠DAC=15°，…（2分）
所以
=
，得AD=100
，…（5分）
在直角△AOD中，∠ADO=45°，所以AO=100（米）； …（7分）
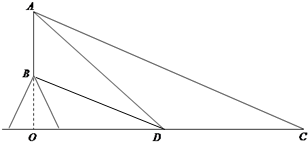
（2）设∠ADO=α，∠BDO=β，由（1）知，BO=48米，
则tanα=
，tanβ=
，…（9分）
tan∠ADB=tan（α-β）=
=
=
，…（11分）
所以tan∠ADB=
≤
=
，…（13分）
当且仅当x=
即x=40
亦即DO=40
时，
tan∠ADB取得最大值，…（14分）
此时点D处观测信号塔AB的视角∠ADB最大． …（15分）
所以
| CD |
| sin15° |
| AD |
| sin30° |
| 2 |
在直角△AOD中，∠ADO=45°，所以AO=100（米）； …（7分）
（2）设∠ADO=α，∠BDO=β，由（1）知，BO=48米，
则tanα=
| 100 |
| x |
| 48 |
| x |
tan∠ADB=tan（α-β）=
| tanα-tanβ |
| 1+tanα•tanβ |
| ||||
1+
|
| 52x |
| x2+4800 |
所以tan∠ADB=
| 52 | ||
x+
|
| 52 | ||||
2
|
13
| ||
| 60 |
当且仅当x=
| 4800 |
| x |
| 3 |
| 3 |
tan∠ADB取得最大值，…（14分）
此时点D处观测信号塔AB的视角∠ADB最大． …（15分）
点评：本题考查正弦定理，考查两角和与差的正切函数，突出考查基本不等式的应用，考查分析与运算能力，属于中档题．
练习册系列答案
相关题目
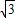-1）米时，测得塔顶A的仰角为45°．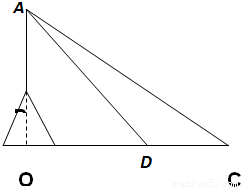
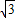-1）米时，测得塔顶A的仰角为45°．