题目内容
设函数 ,则下列结论正确的是
,则下列结论正确的是
- A.函数f(x)的图象关于直线
 对称
对称 - B.函数f(x)的图象关于点
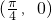 对称
对称 - C.将函数f(x)的图象向左平移
 个单位,得到一个偶函数的图象
个单位,得到一个偶函数的图象 - D.函数f(x)在
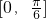 上单调递增
上单调递增
C
分析:求出函数 的对称轴、对称中心、单调增区间,再求出把函数
的对称轴、对称中心、单调增区间,再求出把函数 的图象向左平移
的图象向左平移 个单位后,得到函数y的解析式,从而作出判断.
个单位后,得到函数y的解析式,从而作出判断.
解答:由于函数 的对称轴为2x+
的对称轴为2x+ =kπ+
=kπ+ ,k∈z,即x=
,k∈z,即x= ,k∈z,故排除A.
,k∈z,故排除A.
由于函数 的对称中心的纵坐标等于0,横坐标x满足2x+
的对称中心的纵坐标等于0,横坐标x满足2x+ =kπ,
=kπ,
即x= ,k∈z,故排除B.
,k∈z,故排除B.
把函数 的图象向左平移
的图象向左平移 个单位,得到函数y=2sin[2(x+
个单位,得到函数y=2sin[2(x+ )+
)+ ]=2sin(2x+
]=2sin(2x+ )
)
=cos2x的图象,显然y=cos2x是偶函数,故C满足条件.
由 2kπ- ≤2x+
≤2x+ ≤2k+
≤2k+ ,k∈z,解得 kπ-
,k∈z,解得 kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,
,k∈z,
故函数f(x)在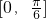 上不具有单调性,故排除D.
上不具有单调性,故排除D.
故选C.
点评:本题主要考查函数y=Asin(ωx+∅)的图象变换,正弦函数的对称性和单调性,属于中档题.
分析:求出函数
 的对称轴、对称中心、单调增区间,再求出把函数
的对称轴、对称中心、单调增区间,再求出把函数 的图象向左平移
的图象向左平移 个单位后,得到函数y的解析式,从而作出判断.
个单位后,得到函数y的解析式,从而作出判断.解答:由于函数
 的对称轴为2x+
的对称轴为2x+ =kπ+
=kπ+ ,k∈z,即x=
,k∈z,即x= ,k∈z,故排除A.
,k∈z,故排除A.由于函数
 的对称中心的纵坐标等于0,横坐标x满足2x+
的对称中心的纵坐标等于0,横坐标x满足2x+ =kπ,
=kπ,即x=
 ,k∈z,故排除B.
,k∈z,故排除B.把函数
 的图象向左平移
的图象向左平移 个单位,得到函数y=2sin[2(x+
个单位,得到函数y=2sin[2(x+ )+
)+ ]=2sin(2x+
]=2sin(2x+ )
)=cos2x的图象,显然y=cos2x是偶函数,故C满足条件.
由 2kπ-
 ≤2x+
≤2x+ ≤2k+
≤2k+ ,k∈z,解得 kπ-
,k∈z,解得 kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,
,k∈z,故函数f(x)在
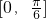 上不具有单调性,故排除D.
上不具有单调性,故排除D.故选C.
点评:本题主要考查函数y=Asin(ωx+∅)的图象变换,正弦函数的对称性和单调性,属于中档题.

练习册系列答案
相关题目
 ,则下列结论正确的是( )
,则下列结论正确的是( ) 的图像关于直线
的图像关于直线 对称
对称 对称
对称 ,且在
,且在 上为增函数
上为增函数 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像 ,则下列结论正确的是
,则下列结论正确的是 的图像关于直线
的图像关于直线 对称
对称 对称
对称 ,且在
,且在 上为增函数
上为增函数 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像 ,则下列结论错误的个数是( )
,则下列结论错误的个数是( ) 的值域为
的值域为 ②
② 对称
对称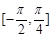 上递增 ④
上递增 ④
 ,则下列结论正确的是
,则下列结论正确的是  的图象关于直线
的图象关于直线 对称
对称  对称
对称 个单位,得到一个偶函数的图象
个单位,得到一个偶函数的图象
 ,且在
,且在 上为增函数
上为增函数 ,则下列结论正确的是
,则下列结论正确的是
 的图象关于直线
的图象关于直线 对称
对称
 对称
对称 个单位,得到一个偶函数的图象
个单位,得到一个偶函数的图象  ,且在
,且在 上为增函数
上为增函数