题目内容
(本小题满分12分)
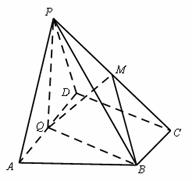如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD//BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M为PC上一点，PA=PD=2，BC=
AD=1，CD=
．
（Ⅰ）求证：平面PQB⊥平面PAD；
（Ⅱ）若二面角M-BQ-C为30°，设PM=
MC，试确定的值.
(本小题满分12分)
证明：（Ⅰ）∵AD // BC，BC=
AD，Q为AD的中点，
∴四边形BCDQ为平行四边形，∴CD // BQ ． ………………… 2分
∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD．
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD， …………………… 4分
∴BQ⊥平面PAD． …………………… 5分
∵BQ
平面PQB，
∴平面PQB⊥平面PAD． ………………… 6分
另证：AD // BC，BC=AD，Q为AD的中点,
∴ BC // DQ 且BC= DQ，
∴ 四边形BCDQ为平行四边形，∴CD // BQ ．
∵ ∠ADC=90° ∴∠AQB=90° 即QB⊥AD．
∵ PA=PD， ∴PQ⊥AD．
∵ PQ∩BQ=Q，∴AD⊥平面PBQ．
∵ AD平面PAD，
∴平面PQB⊥平面PAD．
（Ⅱ）∵PA=PD，Q为AD的中点， ∴PQ⊥AD．
∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，
∴PQ⊥平面ABCD． ………………………… 8分
（不证明PQ⊥平面ABCD直接建系扣1分）
如图，以Q为原点建立空间直角坐标系．
则平面BQC的法向量为
；
，
，
，
．…11分
设
，
则
，
，
∵
，
∴ 
，
∴ 
………… 10分
在平面MBQ中，
，
，
∴ 平面MBQ法向量为
． … 11分
∵二面角M-BQ-C为30°， 
，
∴ 
． ……………… 12分
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
