题目内容
已知 ( )
( )
A. | B. | C. | D. |
A
解析试题分析:由 即
即 ①
①
由 即
即 ②
②
所以①+②可得 即
即 即
即 ,选A.
,选A.
考点:1.同角三角函数的基本关系式;2.两角差的余弦公式.

练习册系列答案
相关题目
如图,函数 (其中
(其中 ,
, ,
, )与坐标轴的三个交点
)与坐标轴的三个交点 、
、 、
、 满足
满足 ,
, ,
, 为
为 的中点,
的中点, ,则
,则 的值为( )
的值为( )
A. | B. | C.8 | D.16 |
为了得到函数 的图像,可以将函数
的图像,可以将函数 的图像( )
的图像( )
A.向右平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向左平移 个单位长度 个单位长度 |
函数
 的部分图象如图所示,若
的部分图象如图所示,若 ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知点 是角
是角 终边上一点,且
终边上一点,且 ,则
,则 的值为( )
的值为( )
| A.5 | B. | C.4 | D. |
方程|x|=cosx在(-∞,+∞)内( )
| A.没有根 | B.有且仅有一个根 |
| C.有且仅有两个根 | D.有无穷多个根 |
已知sin 2α= ,则cos2
,则cos2 =( )
=( )
A.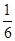 | B. | C. | D. |
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0( ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )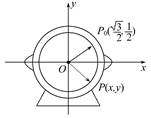
A.y=sin(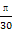 t+ t+ ) ) | B.y=sin(-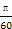 t- t- ) ) |
C.y=sin(-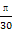 t+ t+ ) ) | D.y=sin(-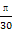 t- t- ) ) |
 在一个周期内的图象如右,此函数的解析式为( )
在一个周期内的图象如右,此函数的解析式为( )
 B.
B.
 D.
D.