题目内容
椭圆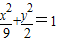 的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则∠F1PF2的大小为 ,△F1PF2的面积为 .
的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则∠F1PF2的大小为 ,△F1PF2的面积为 .
【答案】分析:根据椭圆的方程,可得a=3,b=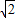 ,c=
,c=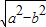 =
=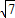 .由椭圆的定义,得|PF2|=2a-|PF1|=2,在△PF1F2中利用余弦定理,可算出∠F1PF2=
.由椭圆的定义,得|PF2|=2a-|PF1|=2,在△PF1F2中利用余弦定理,可算出∠F1PF2=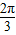 ,最后由正弦定理的面积公式,可得△F1PF2的面积.
,最后由正弦定理的面积公式,可得△F1PF2的面积.
解答:解:∵椭圆的方程为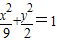 ,
,
∴a2=9,b2=2,可得a=3,b=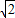 ,c=
,c=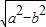 =
=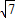
∵|PF1|=4,|PF1|+|PF2|=2a=6,
∴|PF2|=6-|PF1|=2
△PF1F2中,|F1F2|=2c=2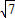 ,
,
∴cos∠F1PF2=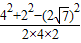 =-
=-
∵∠F1PF2∈(0,π),∴∠F1PF2=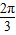
由正弦定理的面积公式,得△F1PF2的面积为S= |PF1|•|PF2|sin
|PF1|•|PF2|sin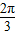 =2
=2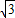
故答案为: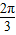 ,2
,2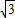
点评:本题给出椭圆的焦点三角形△PF1F2,求∠F1PF2的大小并求面积,着重考查了椭圆的简单几何性质、利用正余弦定理解三角形等知识点,属于基础题.
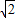 ,c=
,c=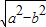 =
=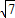 .由椭圆的定义,得|PF2|=2a-|PF1|=2,在△PF1F2中利用余弦定理,可算出∠F1PF2=
.由椭圆的定义,得|PF2|=2a-|PF1|=2,在△PF1F2中利用余弦定理,可算出∠F1PF2=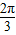 ,最后由正弦定理的面积公式,可得△F1PF2的面积.
,最后由正弦定理的面积公式,可得△F1PF2的面积.解答:解:∵椭圆的方程为
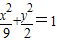 ,
,∴a2=9,b2=2,可得a=3,b=
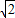 ,c=
,c=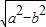 =
=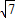
∵|PF1|=4,|PF1|+|PF2|=2a=6,
∴|PF2|=6-|PF1|=2
△PF1F2中,|F1F2|=2c=2
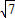 ,
,∴cos∠F1PF2=
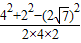 =-
=-
∵∠F1PF2∈(0,π),∴∠F1PF2=
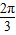
由正弦定理的面积公式,得△F1PF2的面积为S=
 |PF1|•|PF2|sin
|PF1|•|PF2|sin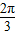 =2
=2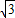
故答案为:
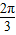 ,2
,2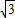
点评:本题给出椭圆的焦点三角形△PF1F2,求∠F1PF2的大小并求面积,着重考查了椭圆的简单几何性质、利用正余弦定理解三角形等知识点,属于基础题.

练习册系列答案
相关题目
