题目内容
已知函数f(x)=ax+bsinx,当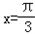 时,f(x)取得极小值
时,f(x)取得极小值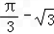 .
.
(1)求a,b的值;
(2)设直线l:y=g(x),曲线S:y=f(x).若直线l与曲线S同时满足下列两个条件:
①直线l与曲线S相切且至少有两个切点;
②对任意x∈R都有g(x)≥f(x).则称直线l为曲线S的“上夹线”.试证明:直线l:y=x+2为曲线S:y=ax+bsinx“上夹线”.
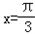 时,f(x)取得极小值
时,f(x)取得极小值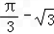 .
.(1)求a,b的值;
(2)设直线l:y=g(x),曲线S:y=f(x).若直线l与曲线S同时满足下列两个条件:
①直线l与曲线S相切且至少有两个切点;
②对任意x∈R都有g(x)≥f(x).则称直线l为曲线S的“上夹线”.试证明:直线l:y=x+2为曲线S:y=ax+bsinx“上夹线”.
解:(1)∵f(x)=ax+bsinx,
∴f′(x)=a+bcosx,
而由已知得: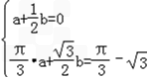 ,
,
∴a=1,b=﹣2,此时f(x)=x﹣2sinx,
∴f′(x)=1﹣2cosx,
当x∈(0,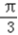 )时,f′(x)<0,
)时,f′(x)<0,
当x∈(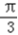 ,
,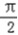 )时,f′(x)>0,
)时,f′(x)>0,
∴当x=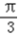 时,f(x)取得极小值
时,f(x)取得极小值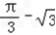 ,
,
即a=1,b=﹣2符合题意;
(2)证明:由f′(x)=1﹣2cosx=1,得cosx=0,
当x=﹣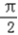 时,cosx=0,
时,cosx=0,
此时y1=x+2=﹣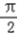 +2,y2=x﹣2sinx=﹣
+2,y2=x﹣2sinx=﹣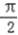 +2,
+2,
∴y1=y2,
∴(﹣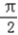 ,﹣
,﹣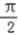 +2)是直线l与曲线S的切点;
+2)是直线l与曲线S的切点;
当x= 时,cosx=0,
时,cosx=0,
此时y1=x+2= +2,y2=x﹣2sinx=
+2,y2=x﹣2sinx= +2,
+2,
∴y1=y2,
∴( ,
, +2)也是直线l与曲线S的切点;
+2)也是直线l与曲线S的切点;
∴直线l与曲线S相切且至少有两个切点,
对任意x∈R,g(x)﹣f(x)=(x+2)﹣(x﹣2sinx)=2+2sinx≥0
即g(x)≥f(x),
因此直线l:y=x+2为曲线S:y=x﹣2sinx“上夹线”.
∴f′(x)=a+bcosx,
而由已知得:
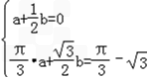 ,
, ∴a=1,b=﹣2,此时f(x)=x﹣2sinx,
∴f′(x)=1﹣2cosx,
当x∈(0,
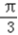 )时,f′(x)<0,
)时,f′(x)<0,当x∈(
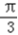 ,
,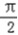 )时,f′(x)>0,
)时,f′(x)>0, ∴当x=
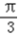 时,f(x)取得极小值
时,f(x)取得极小值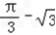 ,
,即a=1,b=﹣2符合题意;
(2)证明:由f′(x)=1﹣2cosx=1,得cosx=0,
当x=﹣
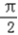 时,cosx=0,
时,cosx=0,此时y1=x+2=﹣
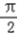 +2,y2=x﹣2sinx=﹣
+2,y2=x﹣2sinx=﹣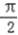 +2,
+2, ∴y1=y2,
∴(﹣
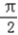 ,﹣
,﹣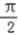 +2)是直线l与曲线S的切点;
+2)是直线l与曲线S的切点;当x=
 时,cosx=0,
时,cosx=0,此时y1=x+2=
 +2,y2=x﹣2sinx=
+2,y2=x﹣2sinx= +2,
+2, ∴y1=y2,
∴(
 ,
, +2)也是直线l与曲线S的切点;
+2)也是直线l与曲线S的切点;∴直线l与曲线S相切且至少有两个切点,
对任意x∈R,g(x)﹣f(x)=(x+2)﹣(x﹣2sinx)=2+2sinx≥0
即g(x)≥f(x),
因此直线l:y=x+2为曲线S:y=x﹣2sinx“上夹线”.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目