题目内容
已知函数f(x)=alnx+ (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若.x1∈(0, ),x2∈(2,∞)且a∈[
),x2∈(2,∞)且a∈[ ,2]时,求证:,f(x1)-f(x2)≥ln2+
,2]时,求证:,f(x1)-f(x2)≥ln2+ .
.
解:(I)由f(x)=alnx+ (a≠0),
(a≠0),
得: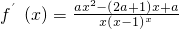 ,
,
∵a≠0,令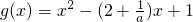 ,
,
∴g(0)=1>0.
令 或
或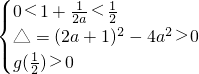 ,
,
则0<a<2.
(II)由(I)得: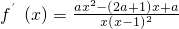 ,
,
设ax2-(2a+1)x+a=0(0<a<2)的两根为α,β,
则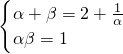 ,得
,得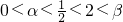 .
.
当x∈(0,α)和(β,+∞)时, ,
,
函数f(x)单调递增;
当x∈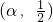 和(2,β)时,
和(2,β)时,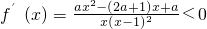 ,
,
函数f(x)单调递减,
则f(x1)≤f(a),f(x2)≥f(β),
则f(x2)-f(x1)≥f(β)-f(α)=alnβ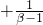 -alnα-
-alnα-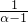
=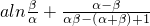
=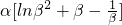 (利用
(利用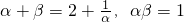 )
)
令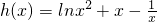 ,x>2
,x>2
则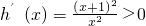 ,
,
则函数h(x)单调递增,
h(x)≥h(2)=2ln2+ ,
,
∴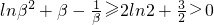 ,
,
∵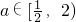 ,
,
则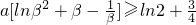 ,
,
∴f(x1)-f(x2)≥ln2+ .
.
分析:(I)由f(x)=alnx+ (a≠0),得:
(a≠0),得: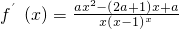 ,由a≠0,令
,由a≠0,令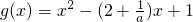 ,知g(0)=1>0.由此能求出实数a的范围.
,知g(0)=1>0.由此能求出实数a的范围.
(II)由(I)得: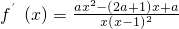 ,设ax2-(2a+1)x+a=0(0<a<2)的两根为α,β,则
,设ax2-(2a+1)x+a=0(0<a<2)的两根为α,β,则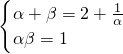 ,得
,得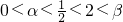 .由此入手能够证明f(x1)-f(x2)≥ln2+
.由此入手能够证明f(x1)-f(x2)≥ln2+ .
.
点评:本题考查实数的取值范围的求法和不等式的证明,考查利用导数求闭区间上最值的应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
 (a≠0),
(a≠0),得:
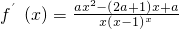 ,
,∵a≠0,令
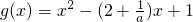 ,
,∴g(0)=1>0.
令
 或
或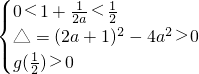 ,
,则0<a<2.
(II)由(I)得:
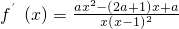 ,
,设ax2-(2a+1)x+a=0(0<a<2)的两根为α,β,
则
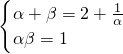 ,得
,得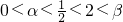 .
.当x∈(0,α)和(β,+∞)时,
 ,
,函数f(x)单调递增;
当x∈
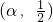 和(2,β)时,
和(2,β)时,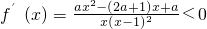 ,
,函数f(x)单调递减,
则f(x1)≤f(a),f(x2)≥f(β),
则f(x2)-f(x1)≥f(β)-f(α)=alnβ
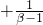 -alnα-
-alnα-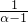
=
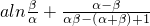
=
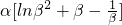 (利用
(利用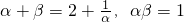 )
)令
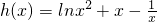 ,x>2
,x>2则
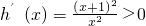 ,
,则函数h(x)单调递增,
h(x)≥h(2)=2ln2+
 ,
,∴
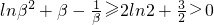 ,
,∵
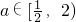 ,
,则
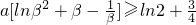 ,
,∴f(x1)-f(x2)≥ln2+
 .
.分析:(I)由f(x)=alnx+
 (a≠0),得:
(a≠0),得: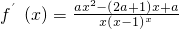 ,由a≠0,令
,由a≠0,令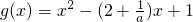 ,知g(0)=1>0.由此能求出实数a的范围.
,知g(0)=1>0.由此能求出实数a的范围.(II)由(I)得:
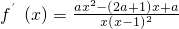 ,设ax2-(2a+1)x+a=0(0<a<2)的两根为α,β,则
,设ax2-(2a+1)x+a=0(0<a<2)的两根为α,β,则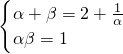 ,得
,得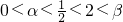 .由此入手能够证明f(x1)-f(x2)≥ln2+
.由此入手能够证明f(x1)-f(x2)≥ln2+ .
.点评:本题考查实数的取值范围的求法和不等式的证明,考查利用导数求闭区间上最值的应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目