题目内容
在等差数列{an}中,(Ⅰ)已知a1=
 ,d=-
,d=- ,Sn=-5,求n及an;
,Sn=-5,求n及an;(Ⅱ)已知d=2,n=15,an=-10,求a1及Sn.
【答案】分析:(1)由求和公式可得关于n的方程,解之可得n,代入通项公式可得答案;(2)由an=a1+(n-1)d代入数据可得a1=-18,代入求和公式可得.
解答:解:(1)由题意可得Sn=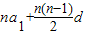
=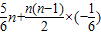 =-5,
=-5,
整理可得n2-11n-60=0,
解之可得n=15,或n=-4(舍去),
an=a1+(n-1)d=1-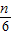
(2)由an=a1+(n-1)d代入数据可得
10=a1+14×2,故a1=-18,
故Sn=S15=18×15+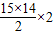 =480
=480
点评:本题考查等差数列的通项公式和求和公式,属基础题.
解答:解:(1)由题意可得Sn=
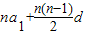
=
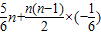 =-5,
=-5,整理可得n2-11n-60=0,
解之可得n=15,或n=-4(舍去),
an=a1+(n-1)d=1-
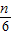
(2)由an=a1+(n-1)d代入数据可得
10=a1+14×2,故a1=-18,
故Sn=S15=18×15+
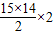 =480
=480点评:本题考查等差数列的通项公式和求和公式,属基础题.

练习册系列答案
相关题目