题目内容
设a为非零实数,函数y=
(x∈R,且x≠-
)的反函数是( )
| 1-ax |
| 1+ax |
| 1 |
| a |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
分析:从条件中函数y=
(x∈R,且x≠-
)中反解出x,再将x,y互换即得原函数的反函数,再依据函数的定义域求得反函数的定义域即可.
| 1-ax |
| 1+ax |
| 1 |
| a |
解答:解:由函数y=
(x∈R,且x≠-
)得:
x=
,
∴函数y=
(x∈R,且x≠-
)的反函数是:
y=
(x∈R,且x≠-1).
故选D.
| 1-ax |
| 1+ax |
| 1 |
| a |
x=
| 1-y |
| a(1+y) |
∴函数y=
| 1-ax |
| 1+ax |
| 1 |
| a |
y=
| 1-x |
| a(1+x) |
故选D.
点评:求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).

练习册系列答案
相关题目
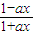 (x∈R,且x≠
(x∈R,且x≠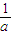 )的反函数是( )
)的反函数是( )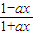 (x∈R,且x≠-
(x∈R,且x≠-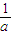 )
)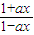 (x∈R,且x≠
(x∈R,且x≠ )
)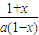 (x∈R,且x≠1)
(x∈R,且x≠1)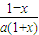 (x∈R,且x≠-1)
(x∈R,且x≠-1)