题目内容
现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.
(1)请你写出总造价y(单位:元)关于底面一边长x(单位:m)的函数解析式y=f(x)及x的取值范围;
(2)请你给出总造价最低的设计方案.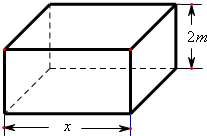
(1)请你写出总造价y(单位:元)关于底面一边长x(单位:m)的函数解析式y=f(x)及x的取值范围;
(2)请你给出总造价最低的设计方案.

(1)∵无盖长方体的深为2m,底面一边长xm,容积为8m3,
∴另一边长为
=
m,
∴S侧=(2x+2×
)×2=(4x+
)(m2),S底=4(m2),
∵池底和池壁的造价分别为120元/m2和80元/m2,
∴总造价y=120×(4x+
)+80×4=480x+
+320(元)(x>0).
(2)∵y=480x+
+320≥2
+320=960×2+320=2240(元).(当且仅当x=2时取“=”).
故该长方体的水池长、宽、高均相等,为2m时总造价最低.
∴另一边长为
| 8 |
| 2x |
| 4 |
| x |
∴S侧=(2x+2×
| 4 |
| x |
| 16 |
| x |
∵池底和池壁的造价分别为120元/m2和80元/m2,
∴总造价y=120×(4x+
| 16 |
| x |
| 1920 |
| x |
(2)∵y=480x+
| 1920 |
| x |
480x?
|
故该长方体的水池长、宽、高均相等,为2m时总造价最低.

练习册系列答案
相关题目
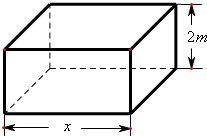 现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.
现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.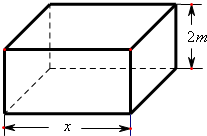 现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.
现要求建造一个容积为8m3,深为2m的长方体无盖水池(如图),如果池底和池壁的造价分别为120元/m2和80元/m2.