题目内容
设数列{an}的前n项和为Sn,且Sn=(m+1)-man对任意正整数n都成立,其中m为常数,m<-1
(1)求证:{an(2)}是等比数列;
(3)设数列{an(4)}的公比q=f(m)(5),数列{bn}(6)满足: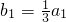 (7),bn=f(bn-1)(8)(n≥2,n∈N)(9),求数列{bnbn+1}(10)的前n(11)项和Tn(12)
(7),bn=f(bn-1)(8)(n≥2,n∈N)(9),求数列{bnbn+1}(10)的前n(11)项和Tn(12)
解:(1)由已知Sn+1=(m+1)-man+1(1)Sn=(m+1)-man(2)
由(1)-(2)得:an+1=man-man+1,
即(m+1)an+1=man对任意n∈N*都成立.∵m为常数,且m<-1.
又∵a1=1≠0∴ ,即数列{an}等比数列(5分)
,即数列{an}等比数列(5分)
(2)当n=1时,a1=(m+1)-ma1,
∴a1=1,从而 ,由(1)得,
,由(1)得,
∴
∴ ,即
,即  .
.
∴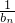 为等差数列,
为等差数列, ,
, ,
,
 =
= ,
,
Tn=b1b2+b2b3+b3b4+…+bnbn+1
=
= .
.
分析:(1)由已知得:an+1=man-man+1,即(m+1)an+1=man对任意n∈N*都成立.所以 ,由此知数列{an}等比数列.
,由此知数列{an}等比数列.
(2)因为a1=1,从而 ,所以
,所以  ,
, ,即
,即  .
.  ,
, ,由此入手能求出Tn.
,由此入手能求出Tn.
点评:本题考查等差数列的证明和数列前n项和的求法,解题时要认真审题,仔细解答,注意递推公式的灵活运用.
由(1)-(2)得:an+1=man-man+1,
即(m+1)an+1=man对任意n∈N*都成立.∵m为常数,且m<-1.
又∵a1=1≠0∴
 ,即数列{an}等比数列(5分)
,即数列{an}等比数列(5分)(2)当n=1时,a1=(m+1)-ma1,
∴a1=1,从而
 ,由(1)得,
,由(1)得,∴

∴
 ,即
,即  .
.∴
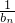 为等差数列,
为等差数列, ,
, ,
, =
= ,
,Tn=b1b2+b2b3+b3b4+…+bnbn+1
=

=
 .
.分析:(1)由已知得:an+1=man-man+1,即(m+1)an+1=man对任意n∈N*都成立.所以
 ,由此知数列{an}等比数列.
,由此知数列{an}等比数列.(2)因为a1=1,从而
 ,所以
,所以  ,
, ,即
,即  .
.  ,
, ,由此入手能求出Tn.
,由此入手能求出Tn.点评:本题考查等差数列的证明和数列前n项和的求法,解题时要认真审题,仔细解答,注意递推公式的灵活运用.

练习册系列答案
相关题目