题目内容
(1)A=N,B=R.f:x→ x∈A,y∈B,f的作用下,
x∈A,y∈B,f的作用下,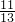 的原象是多少?14的象是多少?
的原象是多少?14的象是多少?
(2)设集合A=N,B={偶数},映射f:A→B把集合A中的元素a映射到集合B中的元素a2-a,则在映射f下,象20的原象是多少?
(3)f:A→B映射,其中A=R,B=(x,y)|x,y∈R,f:x→(x+1,x2+1)则A元素 的象是多少?B元素(2,2)少?
的象是多少?B元素(2,2)少?
解:(1) 由 ,解得 x=6,故
,解得 x=6,故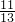 的原象是6;
的原象是6;
又 ,故14的象是
,故14的象是 .
.
(2)由a2-a=20,解得a=5 或 a=-4,
又a∈N,故a=5,即20的原象是5.
(3) 的象是(
的象是( +1,3),
+1,3),
由 ,解得x=1,
,解得x=1,
故(2,2)的原象是1.
分析:(1) 由 ,解得x=6即为所求.
,解得x=6即为所求.
(2)由a2-a=20,解得a 值,再根据a∈N,求得a即为所求.
(3)把x= 代入(x+1,x2+1),可得
代入(x+1,x2+1),可得 的象,由
的象,由 ,解得x值即为(2,2)的原象.
,解得x值即为(2,2)的原象.
点评:本题考查映射的定义,像与原像的定义,让学生不仅会求指定元素象与原象,而且明确求象与原象的方法.
 ,解得 x=6,故
,解得 x=6,故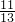 的原象是6;
的原象是6;又
 ,故14的象是
,故14的象是 .
.(2)由a2-a=20,解得a=5 或 a=-4,
又a∈N,故a=5,即20的原象是5.
(3)
 的象是(
的象是( +1,3),
+1,3),由
 ,解得x=1,
,解得x=1,故(2,2)的原象是1.
分析:(1) 由
 ,解得x=6即为所求.
,解得x=6即为所求.(2)由a2-a=20,解得a 值,再根据a∈N,求得a即为所求.
(3)把x=
 代入(x+1,x2+1),可得
代入(x+1,x2+1),可得 的象,由
的象,由 ,解得x值即为(2,2)的原象.
,解得x值即为(2,2)的原象.点评:本题考查映射的定义,像与原像的定义,让学生不仅会求指定元素象与原象,而且明确求象与原象的方法.

练习册系列答案
相关题目