题目内容
证明函数f（x）=x+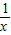
在（1，+∞）上是增函数．
【答案】分析：在区间（1，+∞）上设自变量x1、x2满足x1＜x2，得f（x1）-f（x2）=（x1-x2）（1-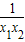
），经讨论得f（x1）-f（x2）＜0，即f（x1）＜f（x2），最后根据函数单调性的定义得函数在（1，+∞）上是增函数．
解答：解：设x1、x2∈（1，+∞），且x1＜x2，得
f（x1）-f（x2）=（x1+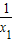
）-（x2-
）
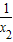=（x1-x2）+（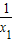
-
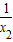）=（x1-x2）（1-
）
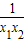∵x1＞1，x2＞1
∴x1x2＞1，得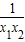
∈（0，1），1-
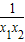＞0
又∵x1＜x2，得x1-x2＜0
∴（x1-x2）（1-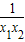
）＜0，可得f（x1）-f（x2）＜0，即f（x1）＜f（x2）
综上所述，可得：函数f（x）=x+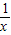
在（1，+∞）上是增函数．
点评：本题给出函数f（x）=x+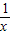
，要求我们用单调性的定义证明函数在（1，+∞）上是增函数．着重考查了用定义证明函数的单调性的一般方法，属于基础题．
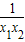），经讨论得f（x1）-f（x2）＜0，即f（x1）＜f（x2），最后根据函数单调性的定义得函数在（1，+∞）上是增函数．解答：解：设x1、x2∈（1，+∞），且x1＜x2，得
f（x1）-f（x2）=（x1+
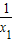）-（x2-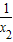）=（x1-x2）+（
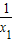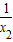-）=（x1-x2）（1-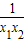）∵x1＞1，x2＞1
∴x1x2＞1，得
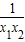∈（0，1），1-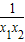＞0又∵x1＜x2，得x1-x2＜0
∴（x1-x2）（1-
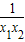）＜0，可得f（x1）-f（x2）＜0，即f（x1）＜f（x2）综上所述，可得：函数f（x）=x+
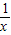在（1，+∞）上是增函数．点评：本题给出函数f（x）=x+
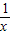，要求我们用单调性的定义证明函数在（1，+∞）上是增函数．着重考查了用定义证明函数的单调性的一般方法，属于基础题． 
练习册系列答案
相关题目
探究函数f(x)=x+
，x∈(0，+∞)的最小值，并确定取得最小值时x的值．列表如下：
请观察表中y值随x值变化的特点，完成以下的问题．
（1）函数f(x)=x+
(x＞0)在区间（0，2）上递减，函数f(x)=x+
(x＞0)在区间 上递增；
（2）函数f(x)=x+
(x＞0)，当x= 时，y最小= ；
（3）函数f(x)=x+
(x＜0)时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
（1）函数f(x)=x+
| 4 |
| x |
| 4 |
| x |
（2）函数f(x)=x+
| 4 |
| x |
（3）函数f(x)=x+
| 4 |
| x |
．
对不小于2的正整数恒成立，求x的取值范围．